1. 서 론
2. 이론적 배경
2.1 원기둥형 전극(Cylindrical electrode)
3. 실내실험 및 결과 분석
4. 고 찰
4.1 반구형전극 사이 거리의 영향
4.2 등가 반구형 전극(Equivalent half-spherical electrode)의 사용으로 인한 영향
5. 결 론
1. 서 론
터널 시공 시에 굴착면 부근에서 대부분 발생하는 터널 붕괴 사고의 주된 요인은 용수나 단층파쇄대 등의 지질 구조와 관련이 있다. 터널 굴진면 붕괴 사고를 사전에 방지하기 위해서는 터널 전방의 지반상태를 정확하게 예측하는 것이 매우 중요하기 때문에, 다양한 현장 탐사 기법들이 적용되고 있다. 시공 중에 터널의 전방을 예측하는 방법은 크게 선진수평시추(probe drilling)를 이용하는 파괴 검사와 탄성파/전기비저항을 이용한 비파괴 검사로 나눌 수가 있다. 선진 수평시추는 전방으로 시추하며 얻어지는 기계데이터 및 코어를 획득하거나 시추공 내에 영상카메라를 관입하여, 지반의 상태와 절리 방향 등을 직/간접적으로 확인하고 분석할 수가 있다(Kim et al., 2015). 하지만 선진수평시추 장비가 매우 크고 코어 획득 및 분석에 많은 시간이 소요될 뿐만 아니라, TBM으로 시공되는 경우에 미리 선진수평시추 장비의 설치공간을 마련해야 하는 단점을 가지고 있다. 탄성파를 이용한 터널 전방 예측 방법들인 TRT (True Reflection Tomography)와 TSP (Tunnel Seismic Prediction) 은 탐사범위가 100 m가량으로 매우 길며 단층 파쇄대 파악에 적합하다(Choi et al., 2004). 하지만 가진 신호(Excitation signal)를 생성하기 위한 발파는 세그먼트 라이닝의 파괴 혹은 진동/소음으로 인한 민원 등의 문제를 야기한다(Yoo et al., 2009; Li et al., 2017). 또한, 2전극 전기비저항을 이용한 터널 전방 예측 방법들은 지질학적인 특성인 함수대와 단층 파쇄대 등의 존재를 터널 직경의 5배가량의 범위 내에서 파악하는데 용이하다(Ryu, 2010; Li et al., 2017).
2전극 전기비저항 탐사법의 하나인 TEPS (Tunnel Electrical resistivity Prospecting System; Ryu, 2010)의 시험절차에서 원지반의 전기비저항 측정 단계는 현재의 지반상태를 정확히 알아야 터널 전방의 지반상태를 상대적인 값의 차이를 활용하여 예측할 수 있기 때문에 매우 중요하다. 원지반의 전기비저항값을 측정하는 순서는, 전극 간 전기저항(R)을 측정하고, 전극과 지반의 총 접촉면적(A)으로부터 반구의 등가 반지름(re)을 계산한 후에(A = 2πre2), 마지막으로 측정된 전기저항과 반구의 반지름의 관계(R ∙ πre)를 이용하여 원지반의 전기비저항을 산출한다(Ryu, 2010). 여기서, 전극의 형상은 지반이 단단한 경우에 천공 후 전극을 삽입하기 때문에 끝이 평평한 전극을 설치하고, 지반이 연약한 경우에는 끝이 뾰족한 원기둥형의 전극을 사용하여 관입을 시킨다. 전극의 형상은 고유의 등전위선(equipotential line)과 전류 흐름(current flow)을 발생시키지만, 이론적인 등전위 표면적(equipotential surface area)을 계산하는 대신에 단순히 반구의 등가 표면적으로만 고려하고 있다. 또한, 4전극 전기비저항 탐사(Wenner 또는 Schlumberger array)도 해석시 계산의 간편성 등의 이유로 실제 전극의 원기둥 형상과는 다르게 점전극(point electrode)으로 취급하여, 전극이 깊이 관입되어 있는 경우에 계산 오차를 야기한다(Baishiki et al., 1987). 이와 함께, 원지반 전기비저항 측정 시에도 전극 사이의 거리나 전극의 형태 및 크기 등에 영향을 받을 것으로 예상되나 아직 반구형의 멀리 떨어진 전극 배열에 대해서만 연구를 진행하였고, 전극 자체에 대한 영향은 연구된 바가 없다. 따라서 본 연구에서는 전극의 형태, 크기와 같은 지오메트리(geometry)와 전극 간의 거리의 따라서 전기 저항을 예측할 수 있는 이론식을 유도하고, 이를 검증하기 위한 실내 실험을 수행하였다.
2. 이론적 배경
2.1 원기둥형 전극(Cylindrical electrode)
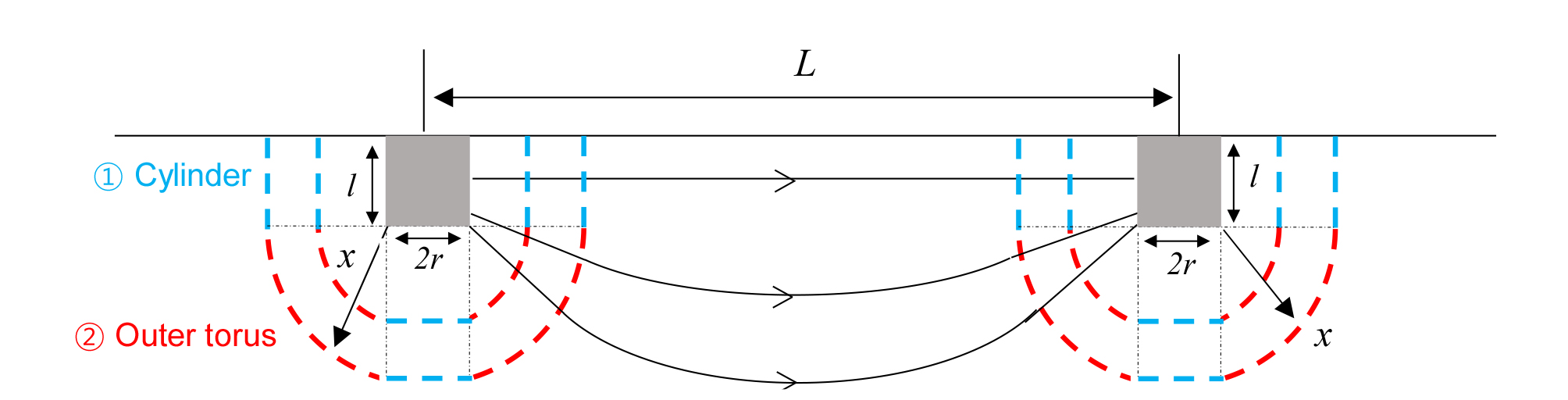
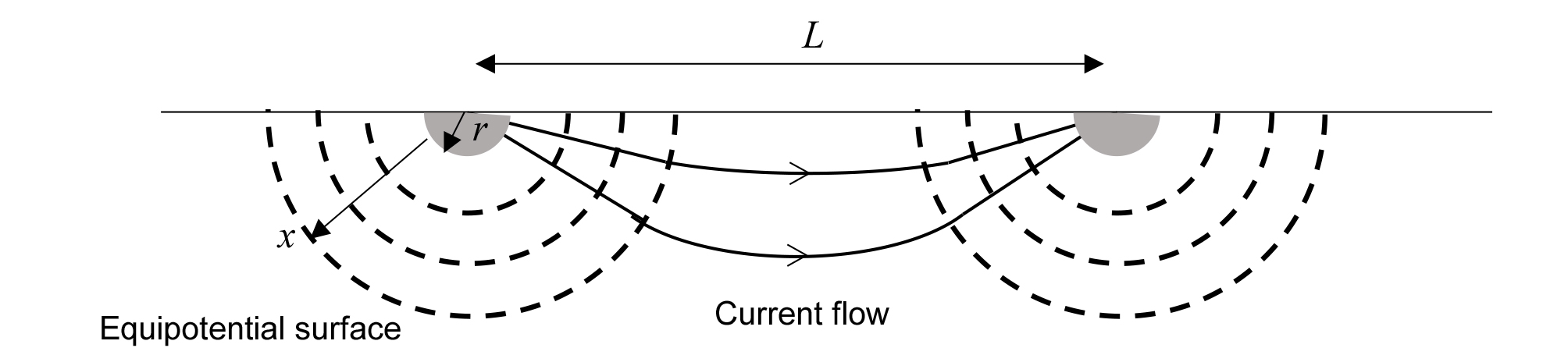
반지름이 r이고, 매질과 접촉하는 관입깊이가 l인 두개의 원기둥형 전극들(동일한 전하량이지만 반대의 극성)이 Fig. 1과 같이 L만큼 떨어져 관입되어 있다고 가정을 하자. 한쪽 전극의 전압은 전극 표면으로부터 임의의 거리 x만큼 떨어진 등전위 표면적 A(x) (equipotential surface area)으로부터 구해지며, 다음 식 (1)과 같이 표현된다.
| $$A(x)=\underbrace{2\pi(r+x)l+\pi r^2+}_{\mathrm{Cylinder}}\underbrace\;_{\mathrm{Half}\;\mathrm{of}\;\mathrm{outer}\;\;\;}$$ | (1) |
V1은 +극성을 가지는 전극의 전압, V2는 -극성을 가지는 전극의 전압이며, 매질의 전기비저항(electrical resistivity)이 ρ, 두 전극 사이에 흐르는 전류(electric current)가 I, 두 전극 사이의 거리가 L인 두 원기둥형 전극 사이의 전압은 다음 식 (2)와 같이 계산된다.
이때, A와 B는 수식의 간편성을 위해 도입된 기호로 아래와 같이 표현된다.
따라서 두 원기둥형 전극 사이의 저항(Rcylindrical)은 다음 식 (3)과 같다.
| $$R_{cylindrical}=\frac\rho{\pi(B-A)}\left[\mathrm{In}\left(\frac{L-2r+A}{L-2r+B}\right)-\mathrm{In}\left(\frac AB\right)\right]$$ | (3) |
3. 실내실험 및 결과 분석
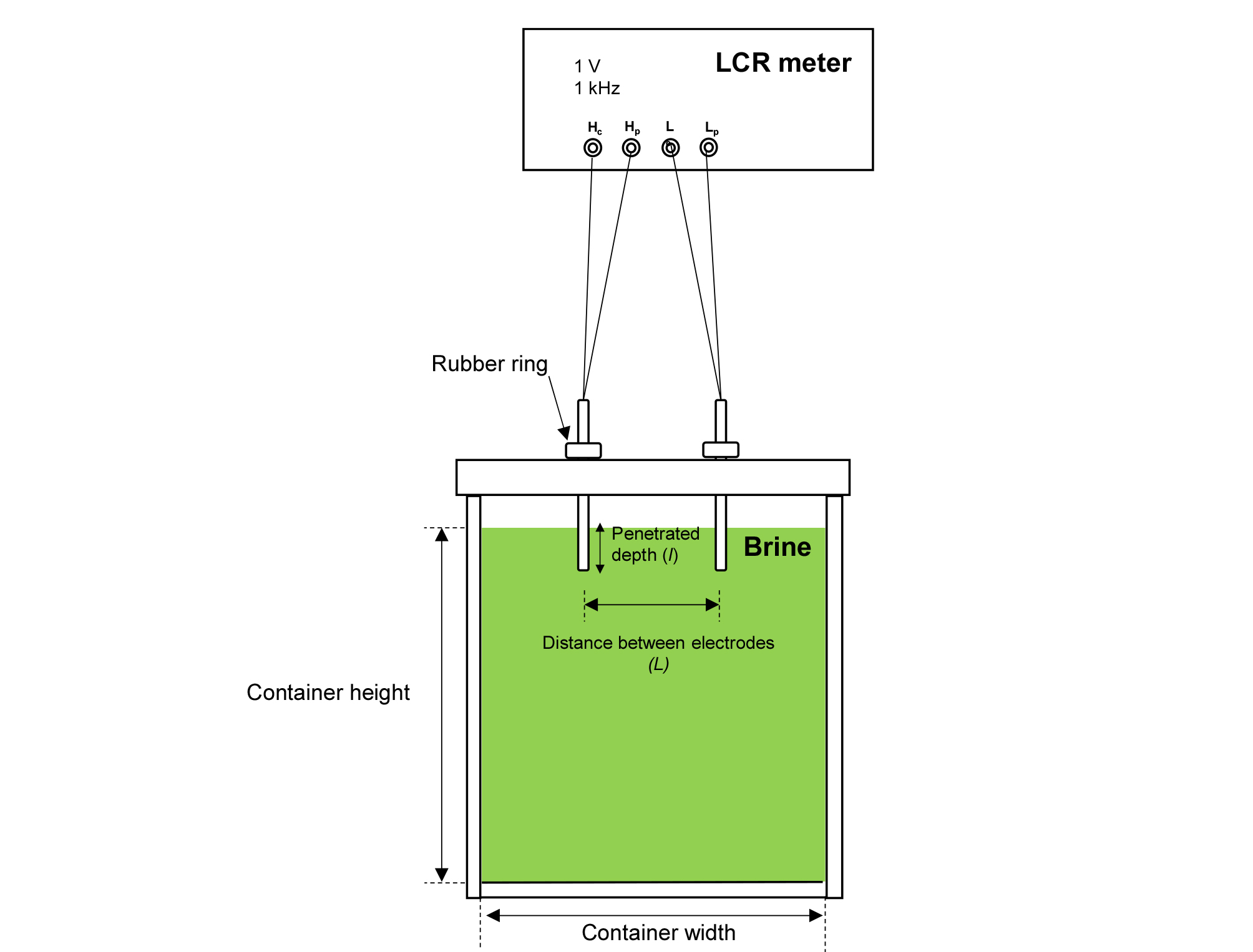
앞서 유도한 이론식들을 검증하기 위하여 실내실험을 수행하였다. 암석이나 토사의 정확한 전기비저항을 실험 도중 정확히 측정할 수 없으므로 전기비저항 값을 실험 도중 측정할 수 있는 액체를 실험의 매질로 사용하였다. 실험에 사용된 액체는 증류수에 소금(NaCl)을 0.1 g과 1 g 넣어 만든 두 소금물(1.18 × 10-5, 1.18 × 10-4 mol)이며 측정된 전기비저항은 각각 52.16, 29.97 Ω × m였다. 실험의 전반적인 구성은 Fig. 2와 같다. 아크릴로 만든 수조의 크기는 0.485 × 0.485 × 0.615 (m), 스테인레스 스틸(SUS 303) 재질로 만들어진 원기둥 형태의 전극은 매질의 접촉깊이 조절과 유지를 용이하게 하기 위해서 고무 링을 사용하였다. 전기비저항의 측정은 conductivity미터(Mettler Toledo S213)를 이용하였고, 전기저항은 LCR미터(Agilent HP 4264B)의 두 채널씩 연결하여 2전극 배열을 만들어 두 전극을 연결하여 분극(Polarization effect)현상을 피할 수 있는 1 V, 1 kHz의 전기신호를 인가하여 측정하였다(Glover et al., 2000). 전극의 관입깊이 l을 5, 10, 20, 40 mm로 바꾸어 가며, 전극의 위치는 수조 중심에서부터 좌우로 20 mm간격으로 이동하며 저항을 측정하였다. 여기서 전극 반지름 r은 4 mm로 고정하였다.
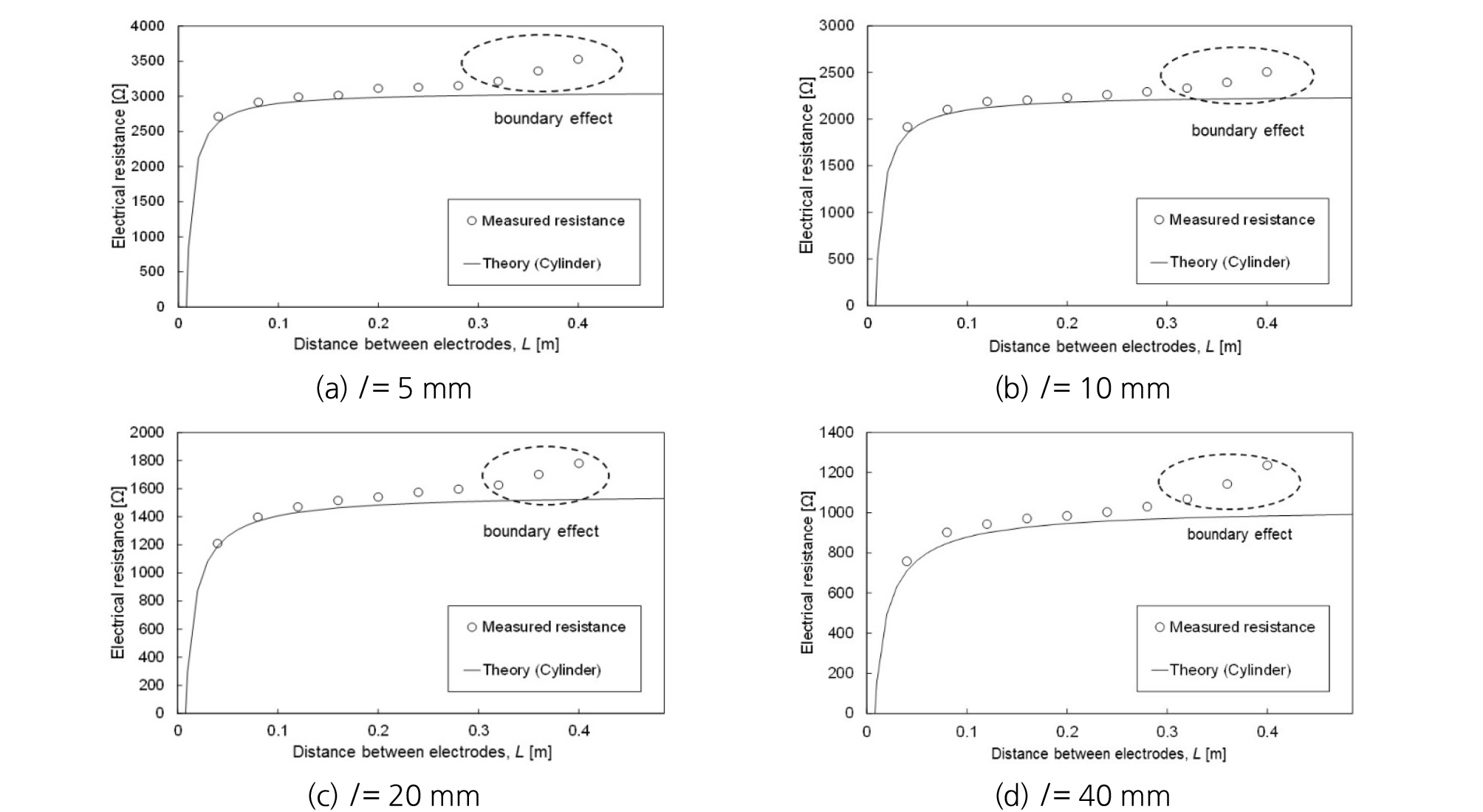
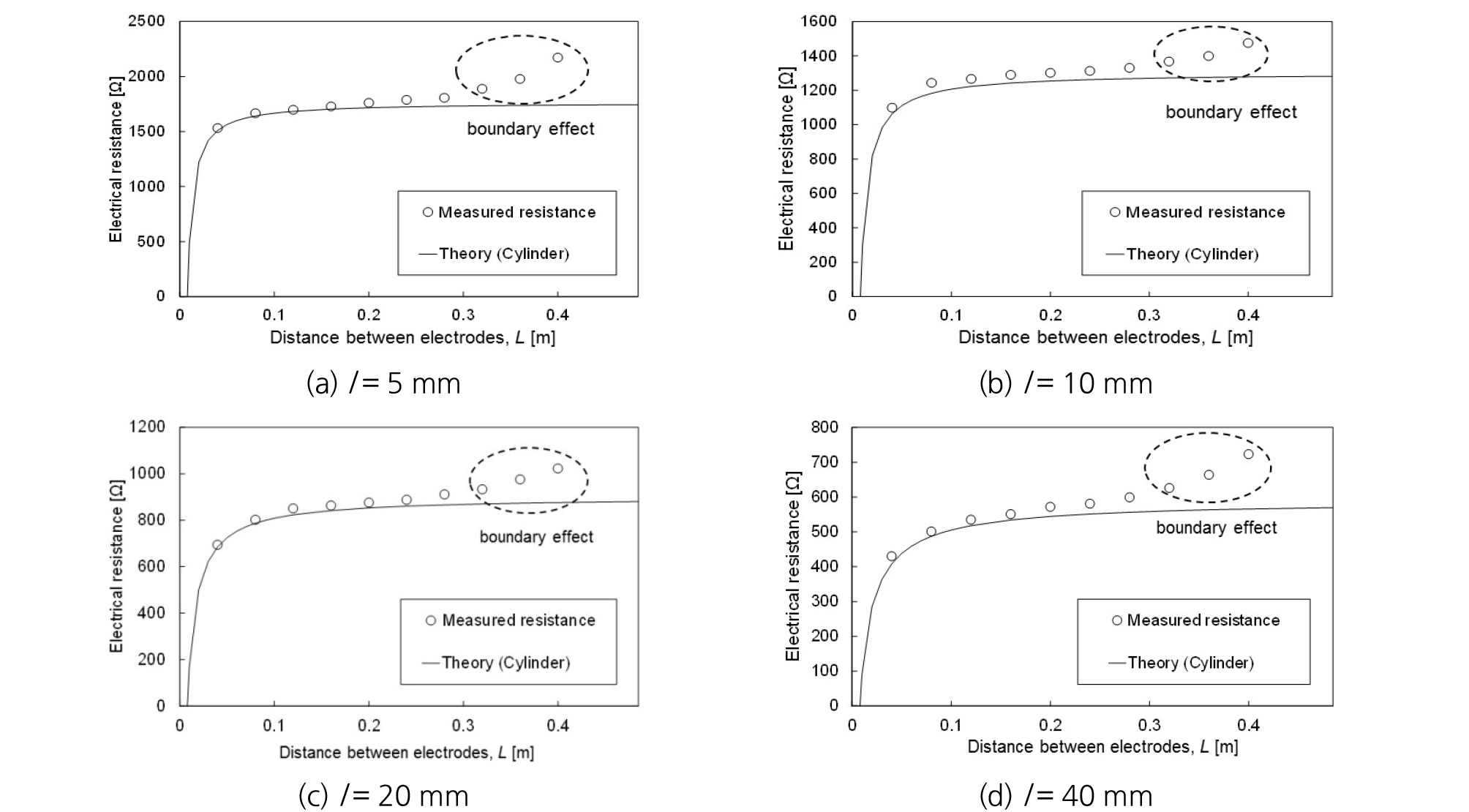
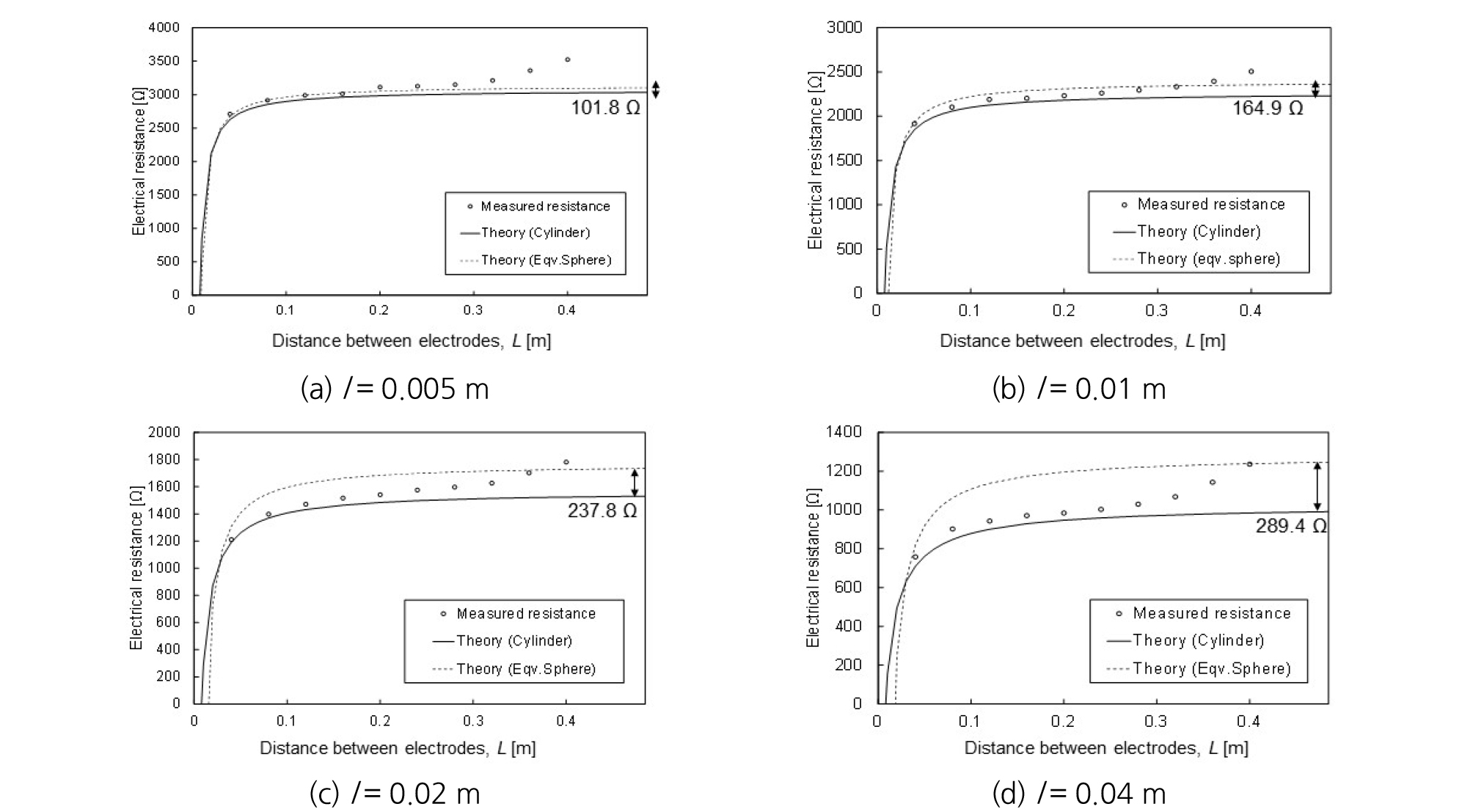
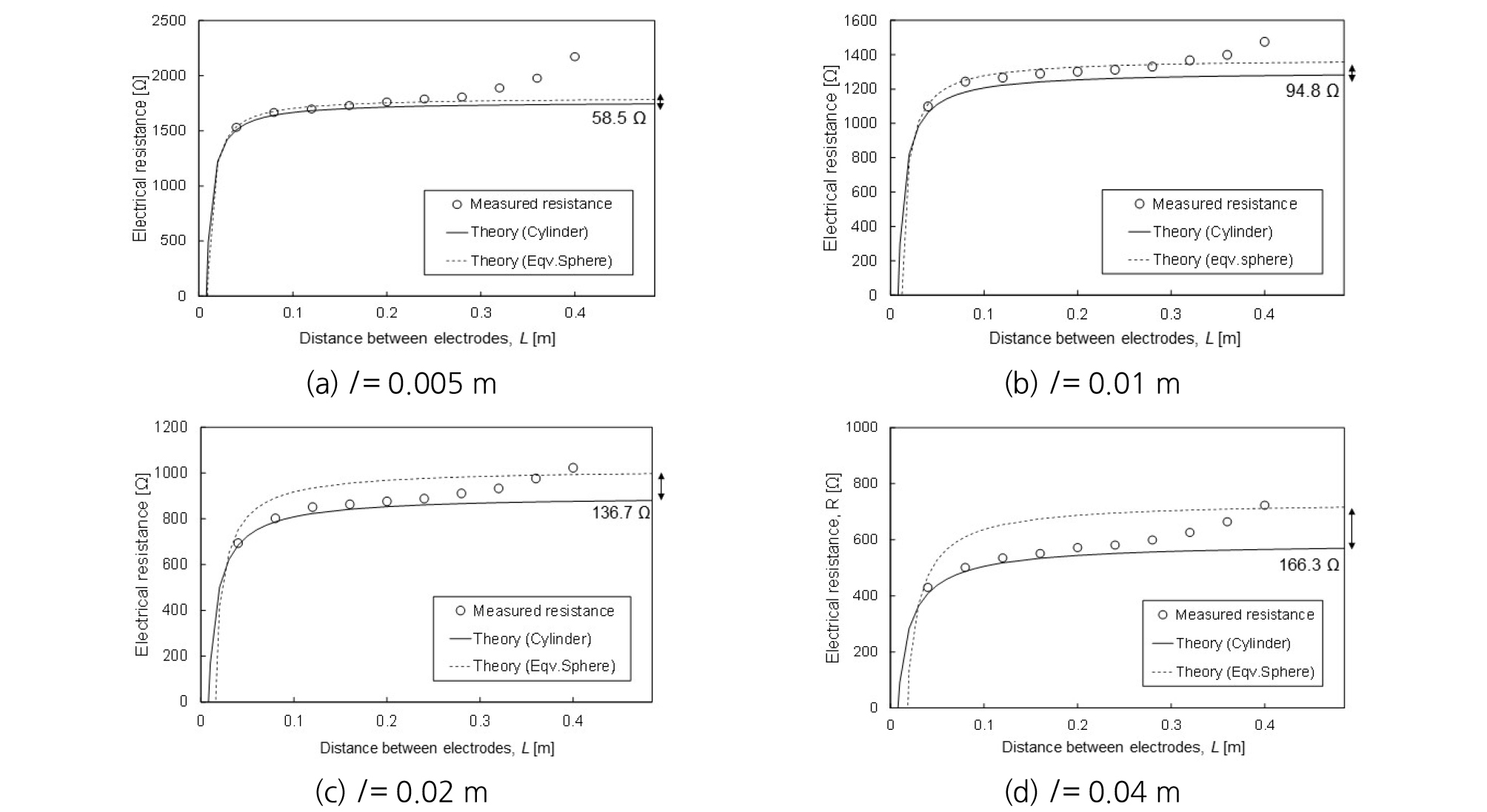
Fig. 3과 Fig. 4는 실내 실험과 이론식을 통해서 구해진 저항값들에 대한 비교를 보여준다. 소금물의 전기비저항이 낮은 경우에 측정되는 전기저항값 역시 작게 측정되었다. 또한, 전극의 잠긴 높이가 증가하면서 측정되는 전기저항값이 감소하였는데, 이는 전극 접촉면적의 증가로 인한 매질을 통과하는 전류속선의 양이 증가하였기 때문이다. 모든 실험케이스들에서 전극 사이의 거리가 약 0.24 m 이내(수조 가로/세로 크기의 절반가량)에서는 이론식으로부터 유도된 전기저항값과 유사하였으나, 그 이상의 거리에서는 실험값이 이론값에 비해 급격히 증가하는 경향을 보였다. 이는 전극들이 점차 부도체(nonconductor) 성질을 가지는 아크릴 수조의 벽면으로 접근함에 따라서 전류의 흐름(current flow)이 방해를 받는 전기적인 경계 영향(electrical boundary effect) 때문으로 판단된다.
4. 고 찰
4.1 반구형전극 사이 거리의 영향
반지름이 r인 두개의 반구형 전극들(동일한 전하량이지만 반대의 극성)이 지표면에서 각각 L만큼 떨어져 있는 곳에 매설되어 있다고 가정을 하자(Fig. 5). 양의 극성을 가진 전극의 전압(V3)과 음의 극성을 가진 전극의 전압(V4)는 각각 전극 표면으로부터 임의의 거리 x만큼 떨어진 등전위 표면적 A(x) (equipotential surface area)으로부터 구해지며, 다음 식 (4)와 같이 표현된다(Fig. 5).
| $$V_{3\;}=V_4=\int_0^{L-2r}\frac{\rho I}{A(x)}dx=\int_0^{L-2r}\frac{\rho I}{2\pi(r+x)^2}dx=\frac{\rho I}{2\pi}\left(\frac1r-\frac1{L-r}\right)$$ | (4) |
여기서, I는 두 전극 사이에 흐르는 전류(electric current), r는 매질의 전기비저항값(electrical resistivity)을 의미한다. 따라서 일정한 전류 I가 흐르는 상태에서 두 반구형 전극 사이의 전기저항 값(Rhalf-sphere)은 두 전극 사이의 전압차를 통해서 구할 수 있다.
| $$R_{half-sphere}=\frac{V_3-V_4}I=\frac\rho\pi\left(\frac1r-\frac1{L-r}\right)$$ | (5) |
두 전극 사이가 충분히 떨어져 측정되는 저항(L→∞)은 ρ/πr로 기존의 연구결과들과 일치하는 것을 확인할 수 있다(Blythe, 1984; Jaschinsky et al., 2008; Ryu, 2010). 또한, 두 전극 사이의 거리가 전극 반지름의 2배인 경우(L = 2r) 두 전극이 접촉하게 되므로 전기저항은 0이 된다.
식 (5)와 기존 연구결과들의 차이를 확인하기 위해 식 (5)의 전기저항값(Rhalf-sphere)을 기존 연구결과의 저항값(RPrevious)인 ρ/πr로 나누어 정규화하였다.
| $$R_{half-sphere}/R_{\Pr evious}=\left(1-\frac1{L/r-1}\right)$$ | (6) |
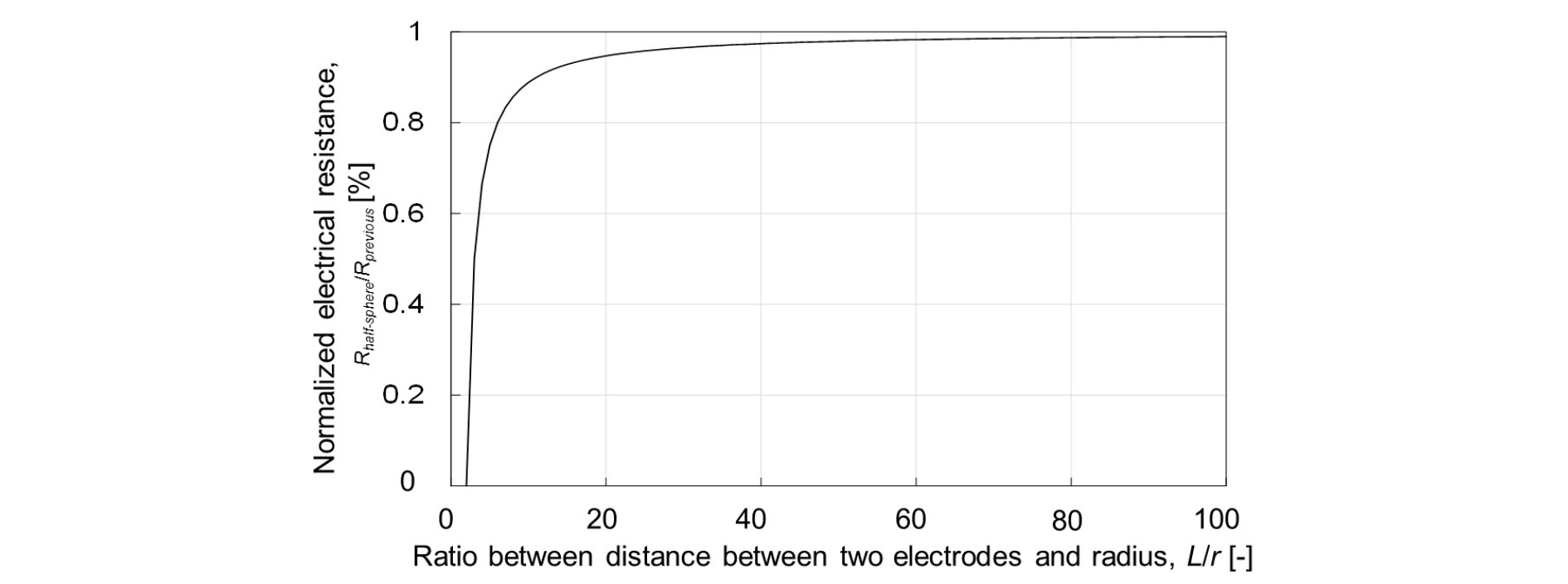
Fig. 6은 전극의 거리 비(ratio)에 따른 정규화된 저항값을 보여준다. L/r이 무한대일 때와 비교하였을 때, L/r이 11일 때 0.9, 51일 때 0.98, 101일 때 0.99수준의 저항값을 보인다. 이는 전극 사이의 거리가 전극의 반지름보다 11배인 경우 ρ/πr 을 식 (5)대신 사용하였을 때 0.1 미만의 오차가 있음을 의미한다.
4.2 등가 반구형 전극(Equivalent half-spherical electrode)의 사용으로 인한 영향
기존 전기 비저항 탐사 방법들에서 대부분 사용되고 있는 등가 반구형 전극 개념은 실제 측정에 사용된 전극의 형상을 등가 반구형 전극의 치환된 반지름과 반구형 전극에서 유도된 이론식을 이용하여 전기비저항을 예측하는 것이다. 등가 반구형 전극의 반지름 re 은 아래와 같은 식 (7)을 통해 얻어진다.
| $$\underbrace{2\pi r_e^2}_{\mathrm{Equivalent}\;\mathrm{half}-\mathrm{sphere}}=\underbrace{2\pi rl+\pi r^2}_{\mathrm{Cylinder}}$$ | (7) |
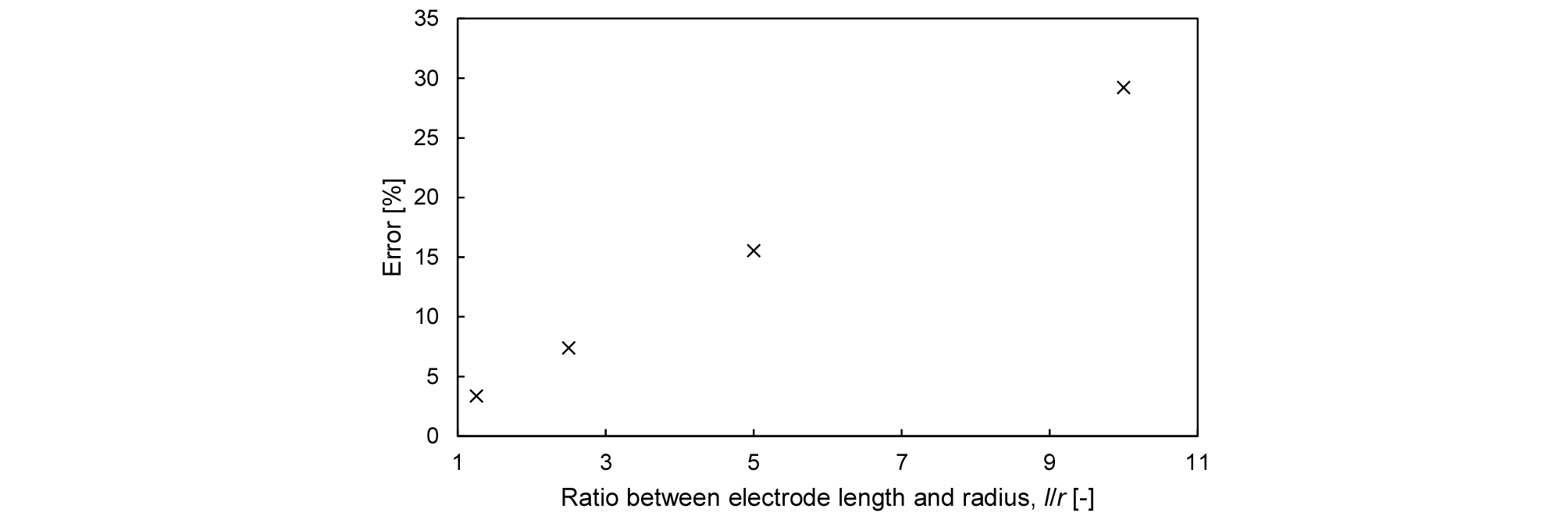
Fig. 7과 Fig. 8은 실제 원기둥형 전극 사이의 저항값 [식 (3), 실선]과 원기둥형 전극과 같은 표면적을 가지는 등가 반구형 전극 사이의 저항값 [식 (5), 점선]을 비교한 결과이다. 실제 전극의 반지름보다 크게 계산되어 두 전극이 접촉하여 전기저항값이 0을 나타내는 전극 사이의 거리 역시 근소하게 증가하였으며, 관입깊이와 반지름의 비(l/r)가 1에 근접하면서 원기둥형 전극과 등가 반구형 전극의 저항값 차이가 줄어들었다. 하지만, l/r 이 1 보다 커지면서 등가 반구형 전극으로 계산된 저항값은 두 전극 사이의 거리가 증가함에 따라서 원기둥 형태의 전극보다 크게 예측되는 경향을 보였다. 두 저항값들의 정량적인 차이를 평가하기 위해 원기둥형 전극과 동일한 면적을 가지는 반구형전극 사이의 거리가 무한대일때의 전기 저항값을 원기둥형 전극의 사이의 거리가 무한대일 때의 전기저항값의 차이를 원기둥형 전극의 전기 저항값으로 나눈 것으로 계산되는 에러(error)와 전극의 지오메트리 비 l/r로 도식화하였다(Fig. 9). l/r 가 1.25에서 10으로 증가함에 따라 원기둥형 전극의 이론값과 원기둥형 전극과 같은 표면적을 가지는 반구형 전극의 이론값의 차이는 3%에서 30%로 증가하였으며, 이는 원기둥형 전극의 관입깊이(l)와 반지름(r)의 비가 5이상으로 큰 경우 오차가 15%이상 발생한다. 이는 l/r이 큰 원기둥형 전극을 이용하여 전기저항 측정 후 매질의 전기비저항 계산 시 반구형 전극으로 가정하기 위해 허용 오차의 범위에 따라 l/r의 비율을 결정해야 함을 의미한다.
5. 결 론
본 연구에서는 터널 굴착면 지반의 전기비저항값을 구하는 과정에서 전극의 크기, 형태 및 배치가 어떠한 영향을 미치는 가를 이론 및 실험적 연구를 통하여 수행하였다. 본 연구에서 얻어진 결론은 다음과 같다.
1. 전기비저항 탐사 시에 주로 사용되는 원기둥형 전극 사이의 전기 저항값은 원기둥형 전극의 반지름, 매질에 관입된 깊이, 전극 중심사이의 거리의 함수를 포함한 이론식으로 표현된다. 두 전극 사이의 거리가 증가하면 측정되는 전기저항값은 전극의 반지름의 크기의 10배 이내에서는 급격히 증가하며, 그 이후에는 완만한 증가를 보이다가 결국에는 일정한 값으로 수렴하게 된다.
2. 아크릴 재질도 만들어진 수조를 이용한 실내 실험과 이론식을 통해서 구해진 저항값들은 소금물의 전기 비저항 값과 전극 사이의 거리가 증가하고 전극이 잠긴 깊이가 감소함에 따라서 증가하였다. 모든 실험케이스들에서 전극 사이의 거리가 약 0.24 m (수조 가로/세로 크기의 절반) 이내에서는 이론식으로부터 유도된 전기저항값과 유사하였으나, 그 이상의 거리에서는 저항값이 급격히 증가하는 경향을 보였다. 이는 전극들이 점차 부도체(nonconductor) 성질을 가지는 아크릴 수조의 벽면으로 접근함에 따라 전류의 흐름(current flow)이 방해를 받는 전기적인 경계 영향(electrical boundary effect) 때문으로 판단된다. 따라서 전기비저항을 이용한 실내실험 설계 시 전극 사이의 거리를 토조의 가로/세로 크기의 절반 이내로 하여 경계 영향을 최소화해야 한다.
3. 원기둥의 길이와 원기둥의 반지름의 비율이 커짐에 따라 식 (3)을 통해 구한 원기둥형 전극 사이의 저항과 식 (5)를 통해 구한 등가 반구형 전극 사이의 저항 차이가 점차 증가하는 경향을 보인다. 그러므로 원기둥형 전극을 원기둥 전극의 면적과 동일한 표면적을 가지는 등가 반구형의 전극으로 취급하기 위해서는 실험 전 식(3)과 (5)를 활용하여 Fig. 9와 같은 오차그래프를 획득한 후 실험에서 허용할 오차 범위 내에서 원기둥의 길이와 반지름의 비율을 결정해야 한다.
본 연구의 결과는 터널 굴착면의 전기비저항 측정뿐만 아니라 지표 전기비저항 측정 시에도 활용할 수 있으며, 전기비저항 측정 시 전극의 크기, 형태 및 배열을 고려하여 탐사를 수행하는 데 도움을 줄 수 있을 것으로 기대된다.