1. 서 론
2. 수치해석
2.1 대표단면 선정
2.2 물성치
2.3 입력지진파
2.4 모델링
3. 결과 및 분석
3.1 터널 단면 거동
3.2 숏크리트 응력
3.3 록볼트
4. 결 론
1. 서 론
2016년, 2017년 발생한 경주와 포항지진으로 인해 발생한 인명재산 피해는 우리나라도 더 이상 지진으로부터 안전지대가 아님을 각인시키는 계기가 되었다. 이후 각종 구조물에 내진설계에 대한 중요성이 크게 대두됨과 동시에 내진설계의 기준이라 할 수 있는 지반 분류 및 설계응답스펙트럼에 대한 연구 또한 활발히 진행되고 있다. 이러한 지진파의 스펙트럼(spectrum)은 실제 지반 및 구조물에 영향을 미치는 요소만을 고려하여 지진파를 스펙트럼화 한 것으로, 이를 결정하기 위해 규모(magnitude), 진앙 거리(epicenter distance), 진원 깊이(focal depth), 주기(period) 등과 같은 요소들이 고려된다. 이 중 지진파의 주기(period)는 구조물에 영향을 주는 매우 중요한 요소 중 하나로 주기특성에 따라 구조물의 피해 정도 및 형태 또한 달라지는 것으로 알려져 있다(Rahgozar, 1993; Goel et al., 1998; Matinmanesh and Asheghabadi, 2011; Shin et al., 2012; Kim et al., 2018, Jang et al., 2018; You and Kim, 2018). 현재 터널의 내진설계에 대한 연구는 터널의 라이닝 설치 후 지반의 interface를 full-slip 또는 no-slip으로 고려하는 지에 대한 연구 및 안정성 평가 방법 등에 초점이 맞춰져 있는 실정이다. 하지만 지진은 터널 시공이 완료된 시점에만 발생하는 것이 아니며, 터널 시공 중에서도 언제든지 발생할 수 있다.
따라서 본 연구에서는 실제 시공 중인 터널을 수치해석으로 모사하여 지진파를 적용함으로써 터널의 거동을 분석하였다. 지진파는 단주기와 장주기로 구분하여 각각 3개씩 선정하였으며, 천단 및 내공변위(crown and spring displacement) 뿐만 아니라 록볼트의 주기 특성에 따른 축력(axial force) 변화 경향을 분석하였다.
본 연구수행을 위해 실제 시공 중인 터널의 계측자료가 이용되었다. 당 현장은 시공 중 단층파쇄대의 출현으로 인해 기준치 이상의 변위가 발생하였다. 따라서 그 안정성 검토 및 재확보를 위해 추가 지반조사를 실시하였으며 그 결과 및 현장계측 자료를 바탕으로 역해석(back analysis)을 수행하여 단층파쇄대의 물성치를 산정하였다. 실제 현장계측 자료와 가장 유사한 상태의 수치해석 결과에 단주기 및 장주기 지진의 파형을 적용하여 동적해석을 수행하였다.
2. 수치해석
2.1 대표단면 선정
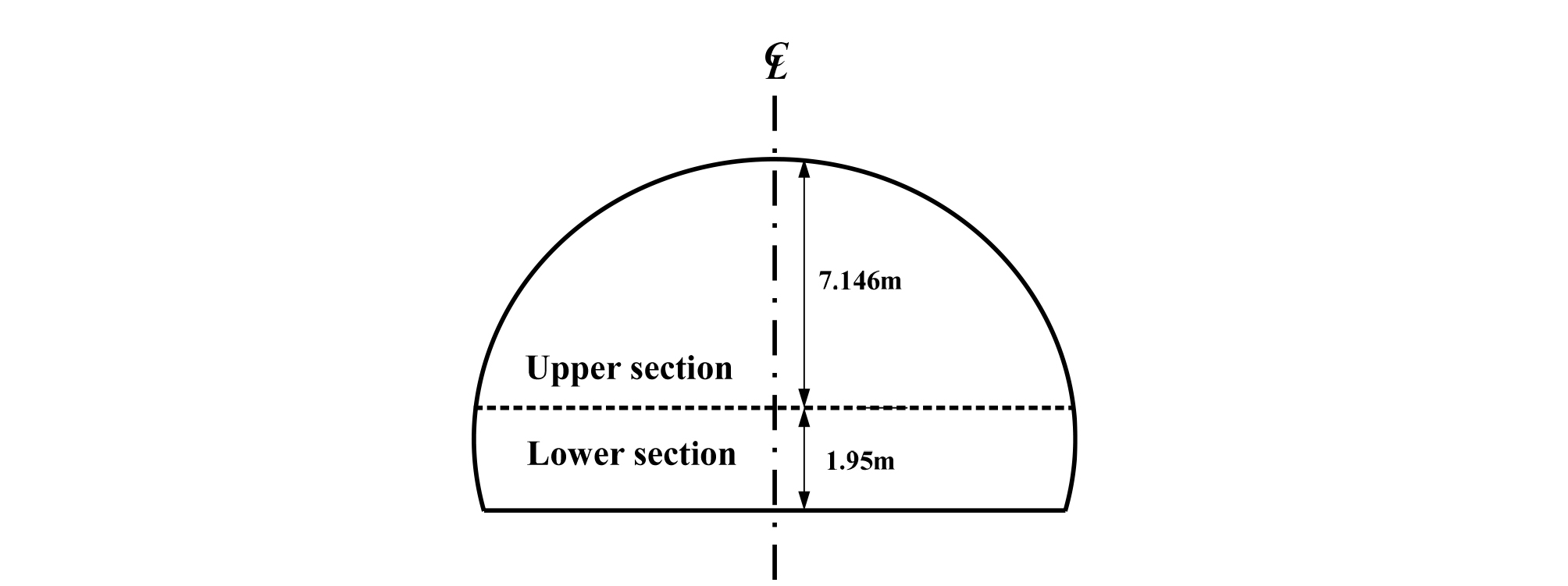
본 연구는 국도 ○호선 건설공사 중 ○○터널을 대상으로 하였다. 터널의 단면은 설계에 적용된 단면을 사용하였으며, 터널의 직경 및 높이는 각각 12.0 m, 9.0 m이다(Fig. 1). 터널굴착은 상반과 하반으로 구분하여 굴착하는 것으로 설계되었으며, 본 연구는 상반굴착 단계에서 발생된 변위를 기준으로 수행되었다. 굴착 후 시공되는 1차 지보재로써 록볼트 및 숏크리트를 사용하였다.
2.2 물성치
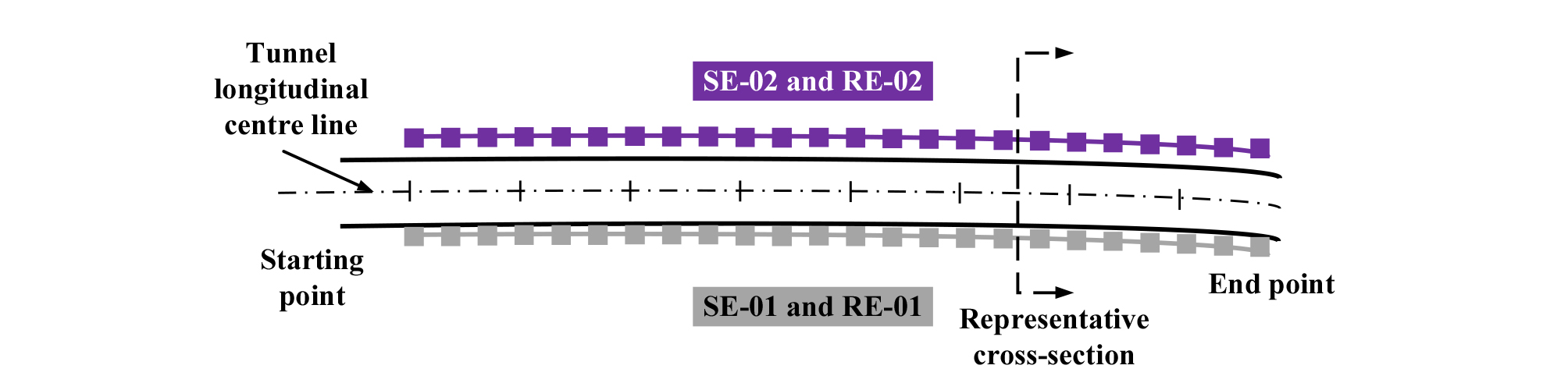
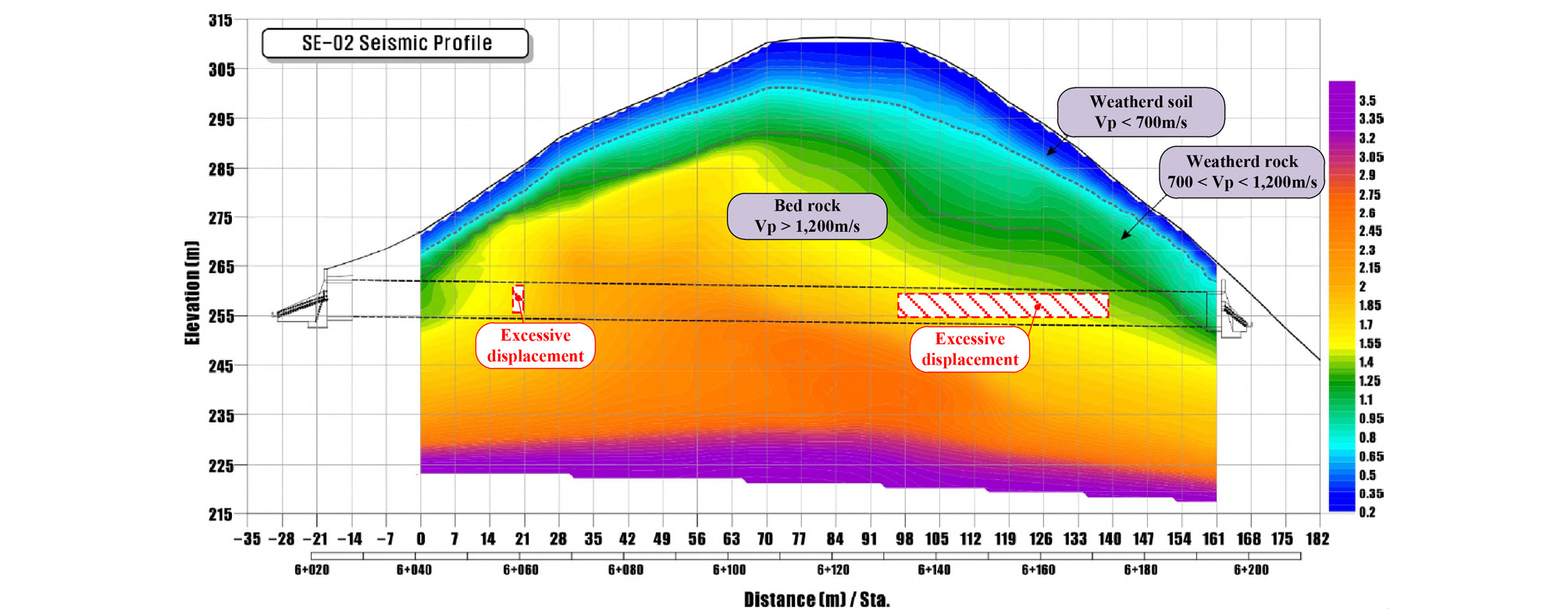
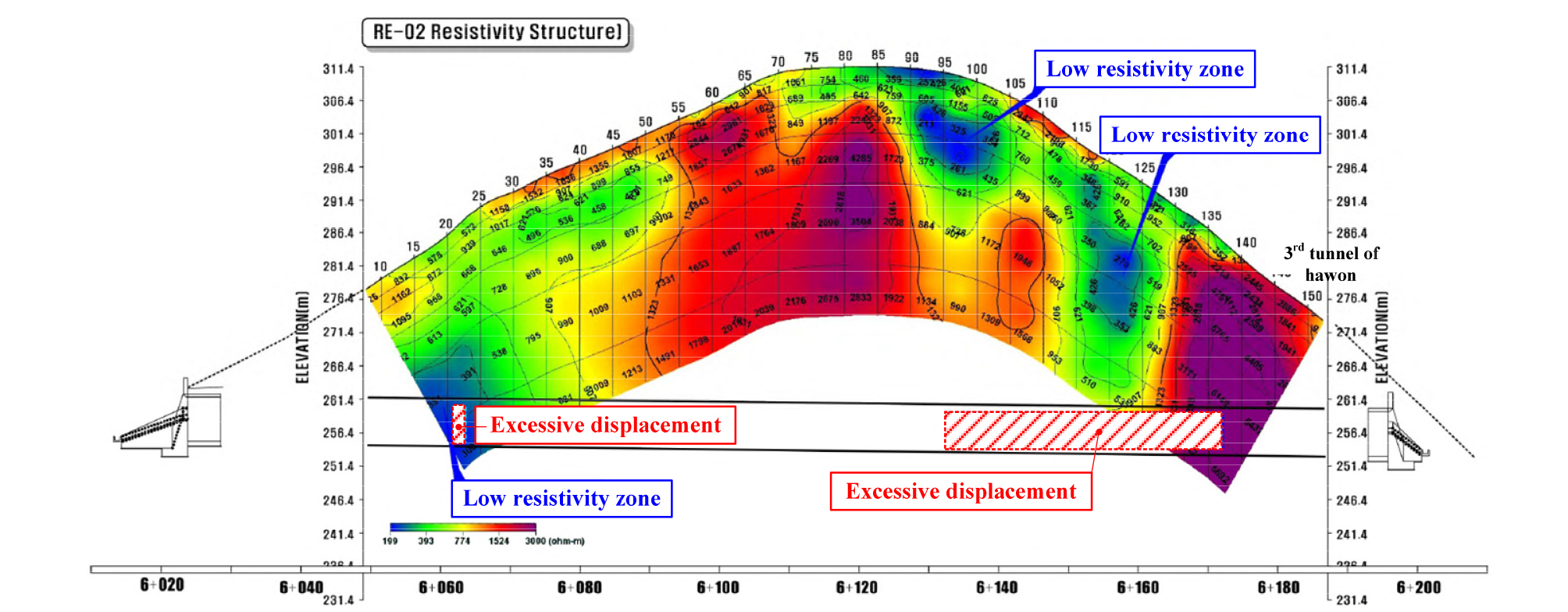
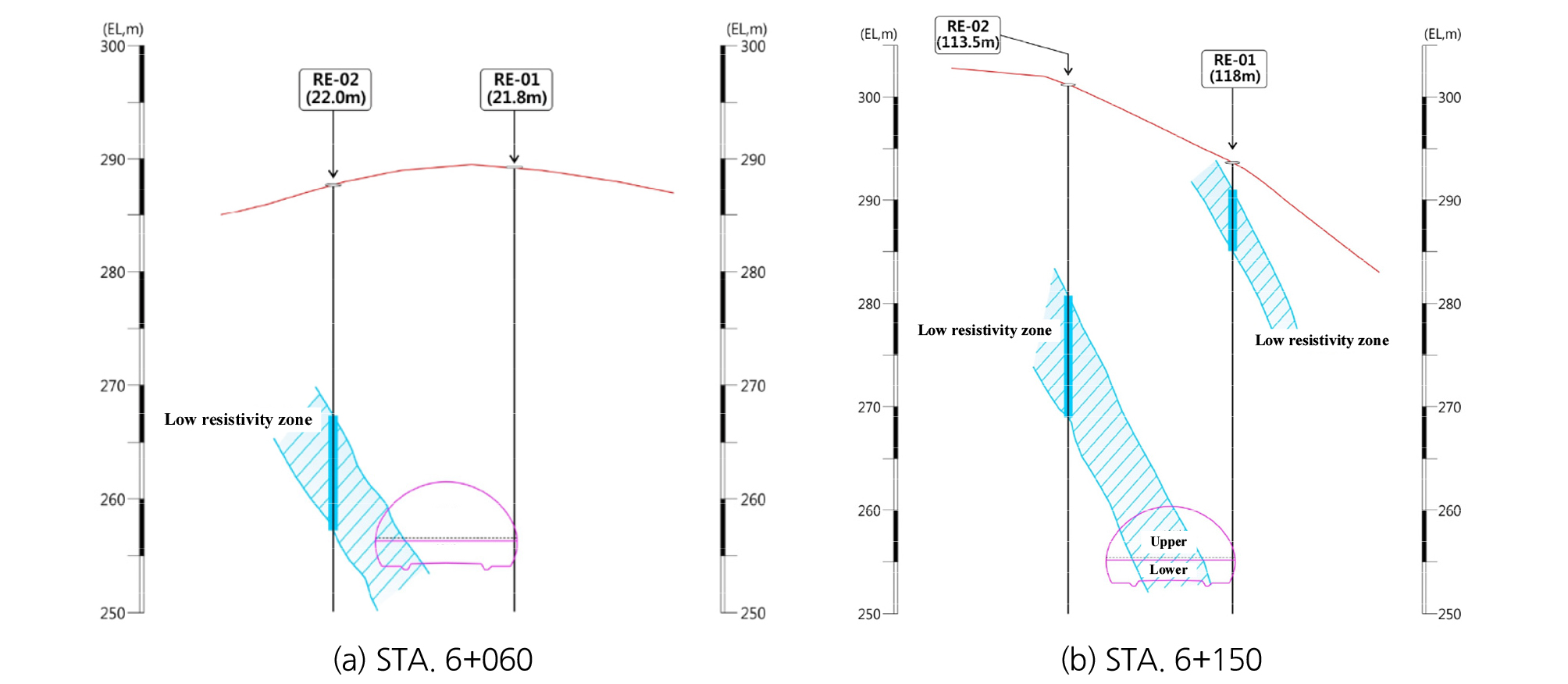
본 연구에서 사용된 지반물성치는 지반조사 결과와 현장계측치를 기준으로 한 역해석 결과를 이용하여 산정되었다. 지반조사는 탄성파탐사, 전기비저항탐사 및 시추조사가 이루어졌으며, 역해석은 단층파쇄대의 강도정수를 산정하기 위한 한계평형해석과 강성계수 산정을 위한 유한요소해석으로 구분되어 수행되었다. 지반재료의 구성모델은 Mohr-Coulomb model, 록볼트 및 숏크리트는 Linear elastic model로 적용되었다. 탄성파탐사 및 전기비저항탐사의 측선은 Fig. 2에 나타내었으며, 각각의 결과를 Fig. 3, 4에 나타내었다. 탄성파탐사 결과 대상단면에서의 토사층 두께는 약 3.0 m, 풍화암층의 두께는 약 6.5 m로 나타났으며, 기반암의 출현심도는 약 9.5 m로 나타났다(Fig. 3). 전기비저항탐사 결과를 통해 파쇄대의 위치 및 규모를 추정할 수 있었으며(Fig. 4), STA. 6+50 및 160구간에서 전기저항이 급격히 떨어지는 구간이 발생되는 것을 알 수 있었다(Fig. 5).
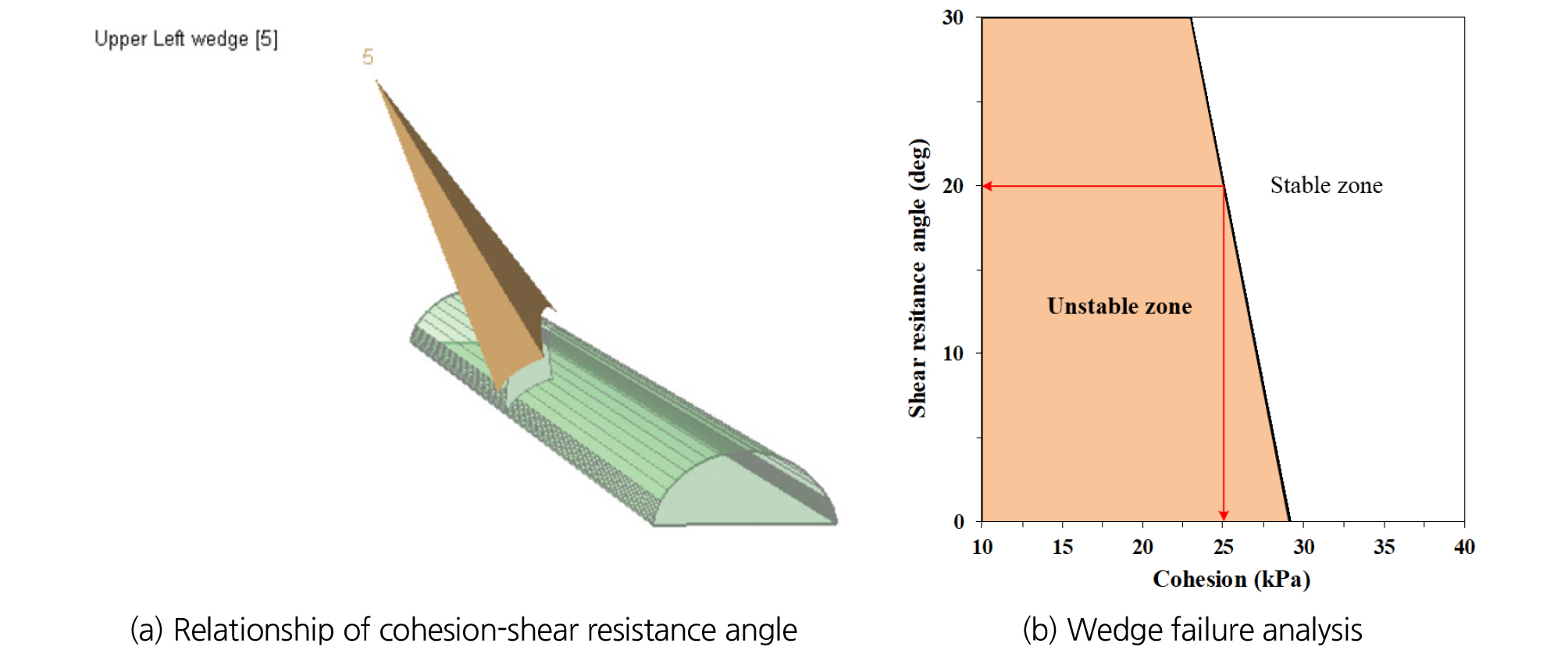
지반조사에서 수행된 지표지질조사 결과를 바탕으로 단층파쇄대로 인해 발생된 터널의 과다변위를 쐐기파괴로 가정하여 한계평형해석을 수행하여 단층파쇄대의 강도정수를 추측하였다. 터널 좌측 및 천단부에서 측정된 주향/절리(단층: 160/58, 165/70, 137/67; 불연속면 1: 230/70, 215/76, 245/70) 결과를 Swedge (Rocsience, ver. 3.005)를 이용하여 모사하였다(Fig. 6(a)).
터널 좌측 및 상부에서 발생된 과다변위를 쐐기파괴로 가정, Swedge (Rocscience, ver. 3.005)를 이용하여 한계평형해석을 수행하였으며, (Fig. 6(a)), 이를 통해 쐐기체의 안전율이 1.0에 근사할 때의 강도정수를 산정하였다(Fig. 6(b)). 점착력은 22.8~29.2 kPa, 내부마찰각은 0~30°까지 고려하여 쐐기체의 안전율이 1.0에 가장 가까울 때의 강도정수를 단층파쇄대의 강도정수로 선정하였다(Table 1).
Table 1. Strength parameter of weathered zone from back analysis
| Cohesion (kPa) | Shear resistance angle (deg) |
| 25.2 | 20 |
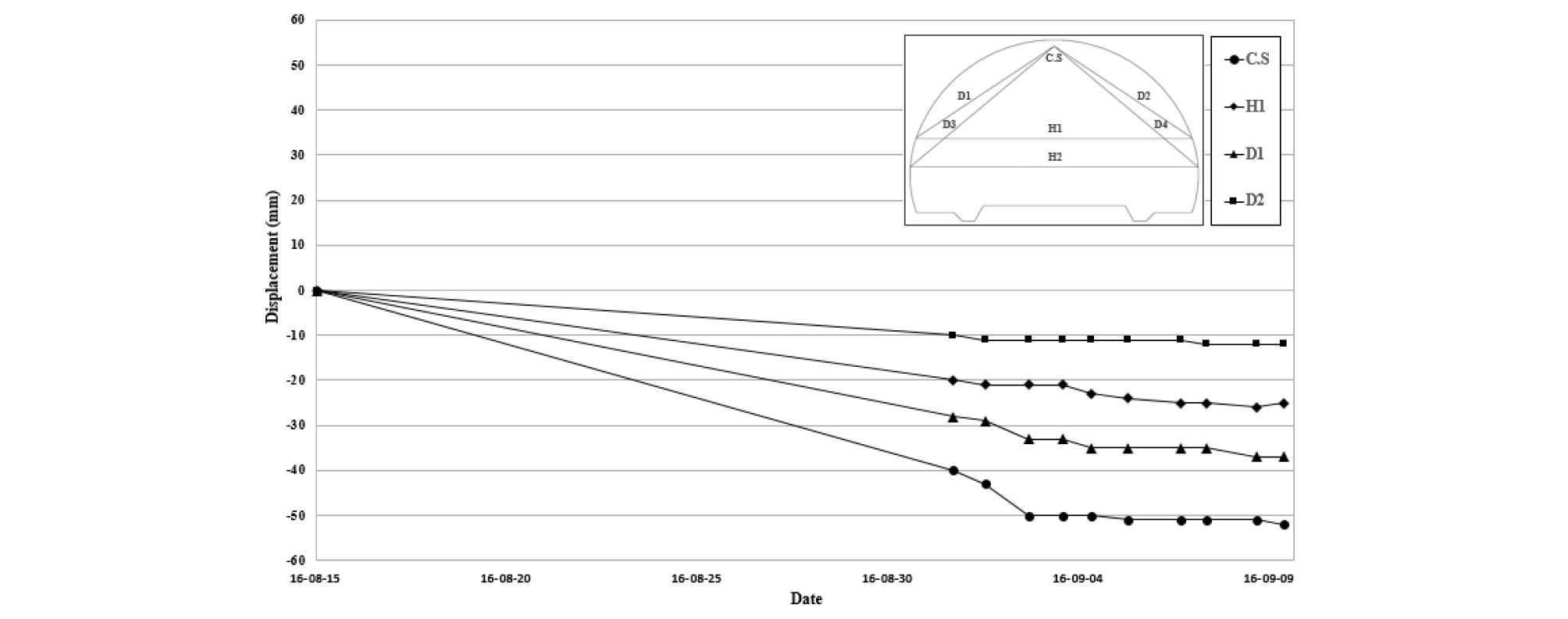
단층파쇄대의 강성계수 산정은 유한요소법을 이용한 역해석을 수행하여 추정하였다. 한계평형해석을 통해 추정된 강도정수를 유한요소해석에 적용하고, 강성계수를 추정하였다. 역해석은 현장계측을 통해 터널 단면의 천단 및 내공변위 값을 기준으로 수행하였으며, 가장 많은 변위가 발생한 터널 종점부(STA. 6+150)의 단면으로 수행하였다. 대상 구간의 경우, 단층파쇄대의 영향으로 인해 시공 중 터널의 천단에서 최대 21.0 mm가 발생하였으며, 좌측부 내공변위는 52.0 mm의 변위가 발생하는 것으로 나타났다(Fig. 7). 이러한 변위는 본 현장의 1차 관리 기준 32.0 mm, 2차 관리 기준 40.0 mm, 3차 관리 기준 50.0 mm를 상회하는 값으로 즉시 시공을 중단하였다. 록볼트의 축력은 천단부 13.5 kN, 좌측부 15.6 kN으로 나타나 각각의 관리기준치인 672 kPa와 69 kN를 넘지 않는 것으로 나타났다. 역해석을 수행하여 터널의 천단변위 19.2 mm, 좌측부 내공변위 57.1 mm, 록볼트의 축력은 천단부 16.1 kN, 좌측부 17.4 kN으로 나타났다. 하지만, 이러한 계측결과는 시공이 진행되던 기간 중에 측정된 결과값이며, 과다변위로 인해 시공이 중단된 상태에서는 터널의 출입이 통제되어 정확한 계측값에 대한 자료는 얻지 못하였다.
록볼트와 숏크리트와 같은 구조요소는 Linear elastic model을 사용하였으며, 사용된 물성치는 Table 2, 3에 정리하였다. 록볼트 및 숏크리트와 같은 구조요소와 지반요소의 경계면에서의 인터페이스는 감소계수(Reduction factor)를 이용하였으며, 록볼트의 경우 지반에 완전히 정착된 것을 가정하여 1.0, 즉, no-slip상태로 모사하였고, 숏크리트는 역해석 과정에서 현장조건과 가장 가까운 0.7을 적용하였다. 풍화암과 단층파쇄대에 적용된 팽창각(ψ)은 Bolton (1986)의 제안식 (ϕ-30)을 이용하였다.
Table 2. Material properties of ground elements
Table 3. Material properties of structure elements
| EA (kN) | EI (kN m2) | Unit weight (kN/m3) | Poisson's ratio (-) | |
| Soft shotcrete | 100e3 | 100 | 23.0 | 0.25 |
| Hard shotcrete | 600e3 | 700 | 23.0 | 0.25 |
| Rockbolt | 148,450 | 8.35 | - | - |
본 연구는 지진하중의 주기 특성에 따라 록볼트의 축력 변화를 분석하는 것이므로, 구조요소의 고유주기 또한 산정되어야 한다. 록볼트와 같은 보강재의 고유주기에 대한 연구는 매우 미미한 실정이다. 따라서 본 연구에서는 RC구조물의 고유주기에 대한 연구를 이용하였다. Lagomarsino (1993), Koo and Kim (2015)은 RC구조물을 대상으로 감쇠비와 고유주기에 대한 연구를 수행하였고, 그 결과 건물의 높이가 100 m 이상일 때는 대부분의 감쇠비가 0.01로 수렴하는 것을 발표했다. 또한 국내 건축설계기준(Architectural Institute of Korea, 2009)에서는 식 (1)과 같은 간편식을 통해 건물의 고유주기를 산정하고 있다.
| $$T=0.073H^{0.75}$$ | (1) |
동적하중을 고려한 수치해석에서 각 지반 재료의 감쇠효과를 고려해야한다. 본 연구에서 사용된 Plaxis (Plaxis bv, ver. 2019.00)는 지반재료의 감쇠효과를 Rayleigh coefficient로 고려한다. Rayleigh coefficient는 각 지반재료의 고유주파수, 감쇠비를 이용하여 산정한다. 지반의 전단파속도는 Sun et al. (2005)의 연구를 이용하였다. 지반의 고유주파수 산정법은 기반암의 깊이가 30 m 이상인지 미만인지 여부를 기준으로 구분되며, 본 연구의 대상 현장의 경우 30 m 미만에 해당되므로, 식 (2)와 같이 고유주기를 산정하고 식 (3)을 이용하여 지반의 고유진동주파수(fsite)를 산정할 수 있다.
| $$T_G=4\sum_{i=1}^n\frac{d_i}{V_{si}}$$ | (2) |
| $$f_{site}=\frac1{T_G}$$ | (3) |
여기서, TG는 지반의 고유주기이며, di는 토층의 두께, VSi는 i번째 토층의 전단파속도(m/s), fsite은 고유주파수이다. 지반의 Rayleigh damping coefficient 산정을 위해 fm,fn을 정의하였다. fn은 1차 모드 주파수로 서, 앞서 산정된 지반의 고유진동주파수(fsite)와 동일하게 가정하였고, fm 은 Kwok et al. (2007)의 연구를 인용하여 5차 모드 주파수로 가정하였다. 토층의 1차 모드와 5차 모드 주파수 fm,fn의 관계를 식 (4)와 같다.
| $$f_m=(2n-1)f_n$$ | (4) |
여기서, n은 모우드 수이다.
감쇠비(ξ)는 기반암의 경우 1%를 적용하였으며, 토사와 풍화암은 5%를 입력하였다. 파쇄대의 감쇠비 또한 5%로 적용하였으며, 록볼트의 감쇠비는 Lee and Kim (2010)의 SC구조의 내진설계를 위한 감쇠비에 대한 연구를 결과를 인용하여 각각 4~7%를 적용하였다.
실제 록볼트의 고유주기를 판단함에 있어 철근콘크리트구조물과 동일하게 고려할 수 있는지 여부는 많은 연구자 및 공학자들에게 논란거리가 될 수 있다고 판단되지만, 현재까지는 록볼트 및 숏크리트의 감쇠비에 대한 연구가 미미한 실정임에도 불구하고 최대한 합리적인 해석 결과를 도출하기 위해 이를 적용하였다. 숏크리트의 감쇠 특성은 고려하지 않았다.
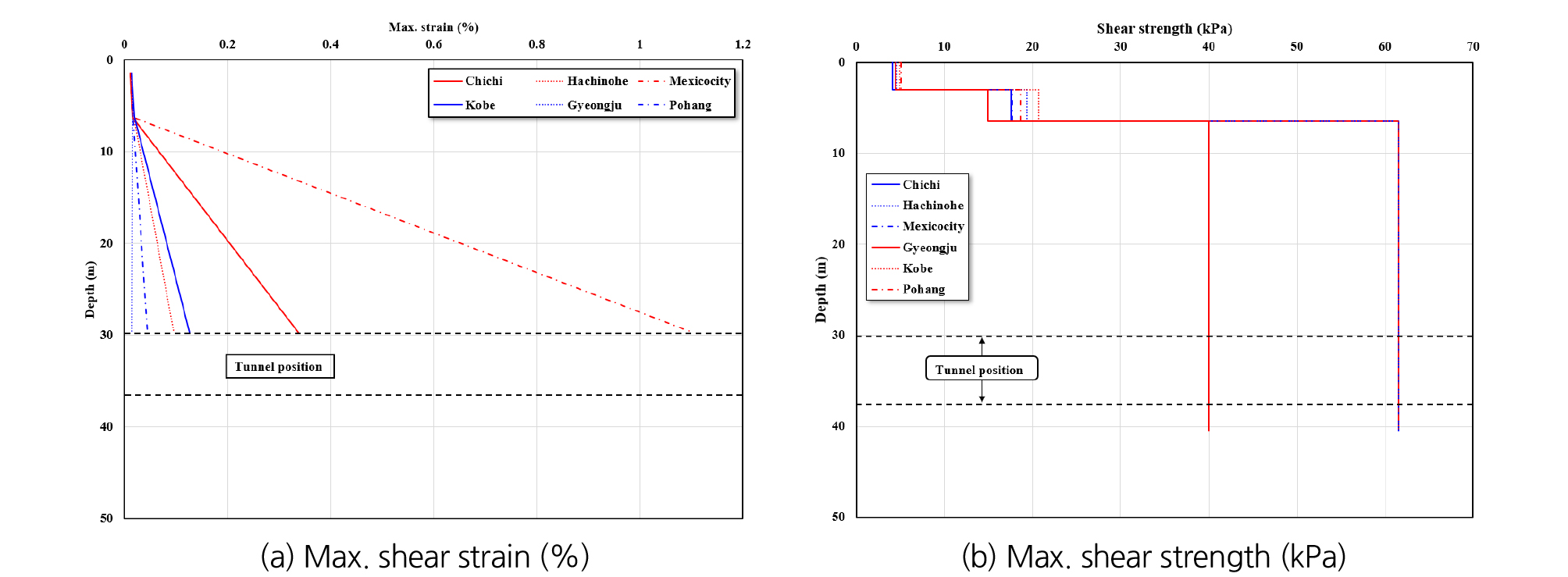
위에서 언급된 방법들로 산정된 지반 및 구조요소들의 Rayleigh damping coefficient를 Table 4에 정리하였다. 지반의 감쇠비 뿐만 아니라 전단탄성계수 또한 동적해석에 영향을 미치는 중요한 인자라고 할 수 있다. 본 연구에서는 1차원 비선형 지반응답해석에 지반별 전단파속도와 정적물성치, 지진파를 입력하여 얻은 깊이에 따른 전단변형률 주상도를 도출하여 적용하였다(Hashash et al., 2017) (Fig. 8).
Table 4. Rayleigh damping coefficient of materials
| α | β | |
| Soil | 4.152 | 2.17e-04 |
| Weathered rock | 5.174 | 1.74e-04 |
| Fracture zone | 0.3523 | 2.56e-03 |
| Bed rock | 0.3178 | 1.13e-04 |
| Rockbolt | 0.1369 | 4.93e-04 |
2.3 입력지진파
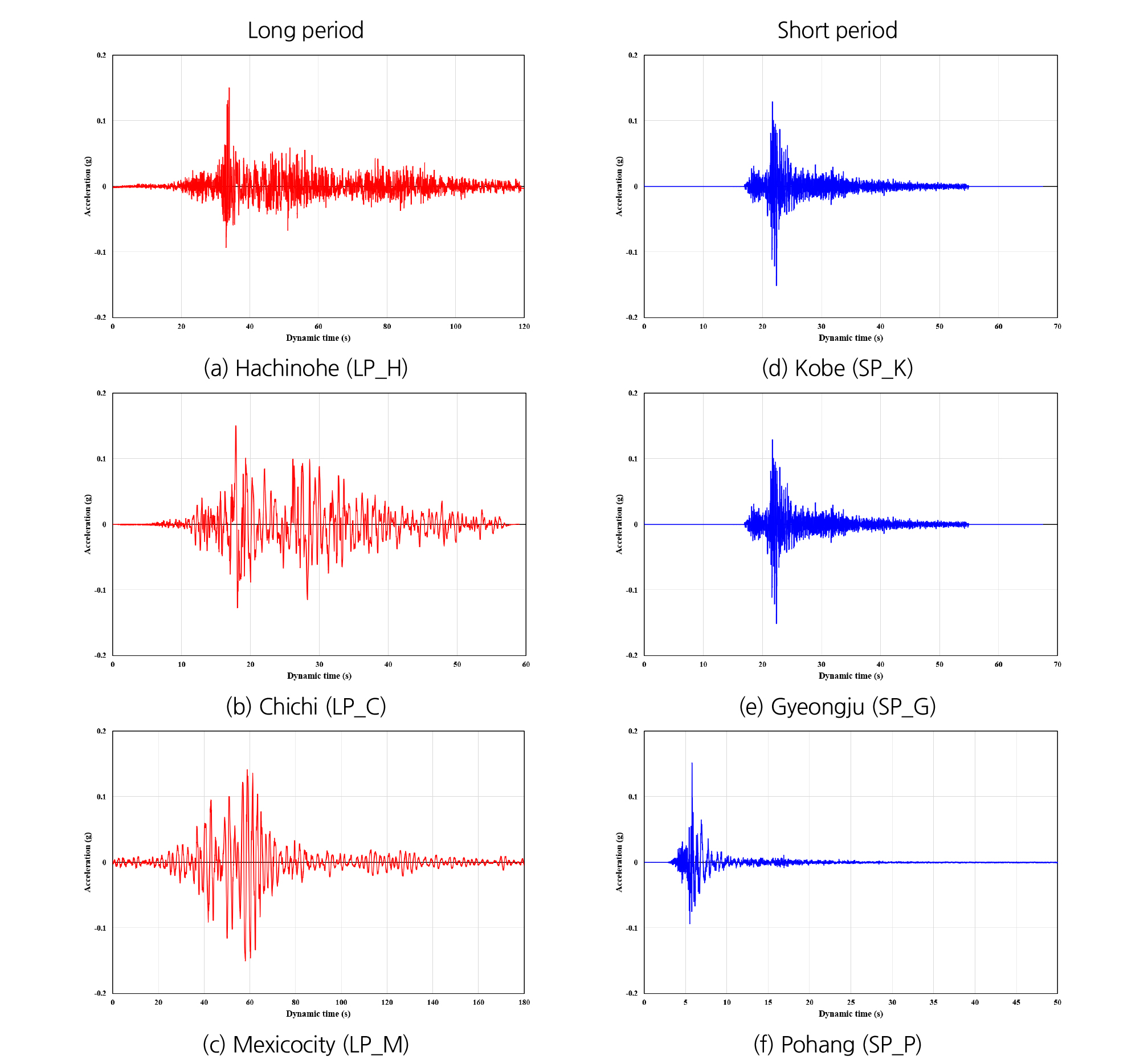
본 연구에서 총 6개의 지진파를 동적하중으로 고려하였다. 지진의 구분은 각 지진파의 주기특성을 기준으로 장주기와 단주기로 구분하였으며, 단주기 지진은 Kobe (Japan, 1995), Gyeongju (Korea, 2016), Pohang (Korea, 2017), 장주기 지진은 Chichi (Taiwan, 1999), Hachinohe (Japan, 1968), Mexico city (Mexico, 1985)의 지진정보를 이용하였다. 지진파는 1000년 재현주기 0.154 g를 기준으로 scalling하여 수치해석에 적용하였다(Fig. 9).
2.4 모델링
본 연구에서는 파쇄대의 물성치 산정을 위한 역해석 과정에서 사용된 터널 단면, 락볼트 길이, 지반조건 등을 동일하게 적용하였으며, 동적하중 고려에 필요한 다양한 요소들을 고려하여 모델링하였다.
Park et al. (2010)은 유한요소(차분)법을 이용한 지진 해석 시 가장 합리적인 경계조건에 대해 언급하였다. 연구에 따르면, 지진해석시 경계조건은 기반암으로부터 전달된 지진의 파형이 반사되지 않지만, 수치해석 모델링 과정에서 경계조건을 올바르지 않게 설정하면 입력된 지진파가 모델링의 경계에서 반사되어 지진으로 인한 실제 지반의 변형에 비해 크게 발생할 수 있어 올바른 분석이 어려울 수 있다. 따라서 경계조건은 하부와 측면부로 구분하여 적용할 수 있으며, 하부의 경우 compliant base (무한경계), 측면부의 경우 free-field 조건으로 모델링하였다. 하부 경계조건에 적용된 compliant base는 지진파를 Deconvolution하여 적용한 결과와 크게 다르지 않으며, 이는 반사된 조건을 반영하기 때문이다. 측면 경계조건에 적용된 free-field는 모델링 경계에서 지진파가 반사되는 것을 방지하기 위해 damper를 적용한 경계조건이다.
또한, 수치해석을 이용한 지진해석시 요소의 크기도 중요한 고려사항 중 하나이다. 유한요소해석에서요소의 크기가 크면 고주파수 대역이 나타나지 않고, 작으면 결과가 불안정하게 나타날 수 있다(Saenger et al., 2000). 따라서 Zerwer (2002)는 최적의 요소크기를 식 (5)와 같이 제안하였다.
| $$\triangle x\leq\chi\cdot\lambda_{min}$$ | (5) |
여기서, Δx는 요소의 크기, χ는 질량행렬상수, λmin는 최소파장으로 전단파속도를 최대주파수로 나눈 값을 의미한다. Song et al. (2008) 에 따르면, 질량행렬상수 χ는 구성방정식이 집중질량행렬을 이용하는 경우 0.2, 일관질량행렬을 사용하는 경우 0.25를 적용한다. 본 연구에서 사용된 Plaxis의 경우 집중질량행렬을 사용하므로 0.2를 적용하였다. 각 지진파의 최대주파수를 구하여 산정된 요소의 Δx는 3.64 m, 즉, Mesh coefficient를 0.333으로 적용하여 요소의 크기를 산정하였다.
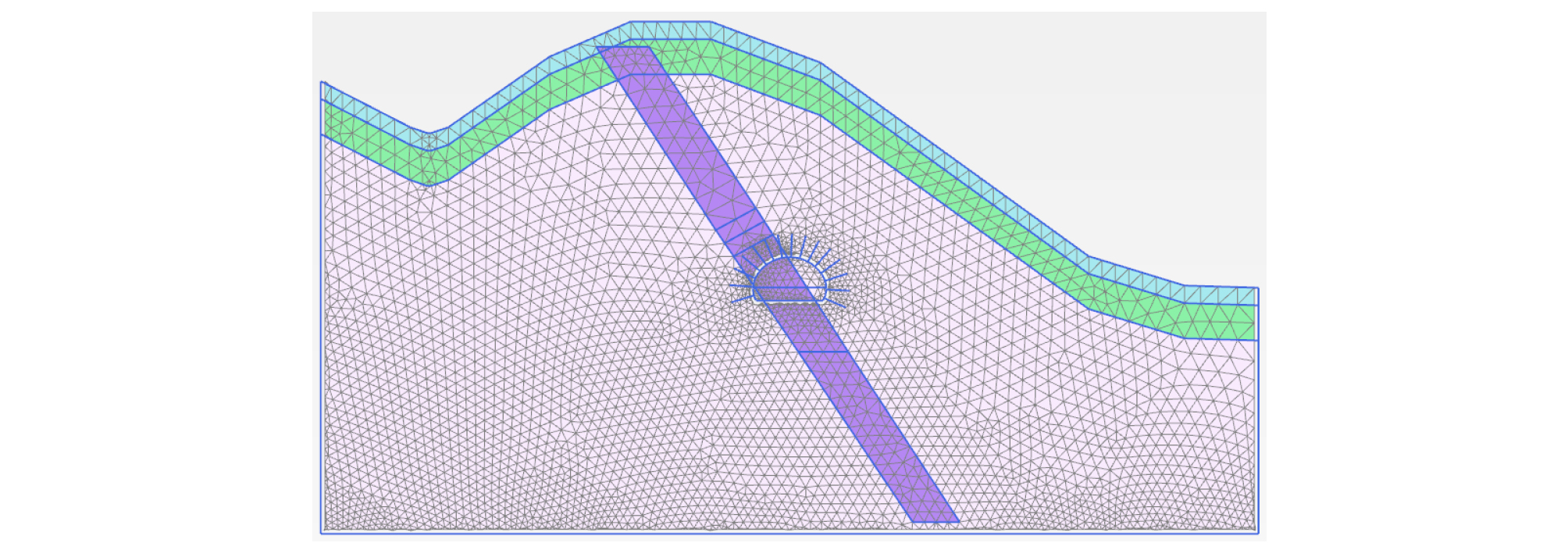
파쇄대의 위치는 앞서 수행한 지반조사(탄성파탐사, 전기비저항탐사) 및 지표지질조사 수행 결과를 통해 나타난 파쇄대의 위치를 모사하였다(Fig. 10).
또한 수치해석과정에서 하중분담율을 고려하였다. 하중분담율은 설계단계에서 선정된 굴착, 연성숏크리트, 강성숏크리트 단계에서 각각 40%, 30%, 30%를 적용하였다.
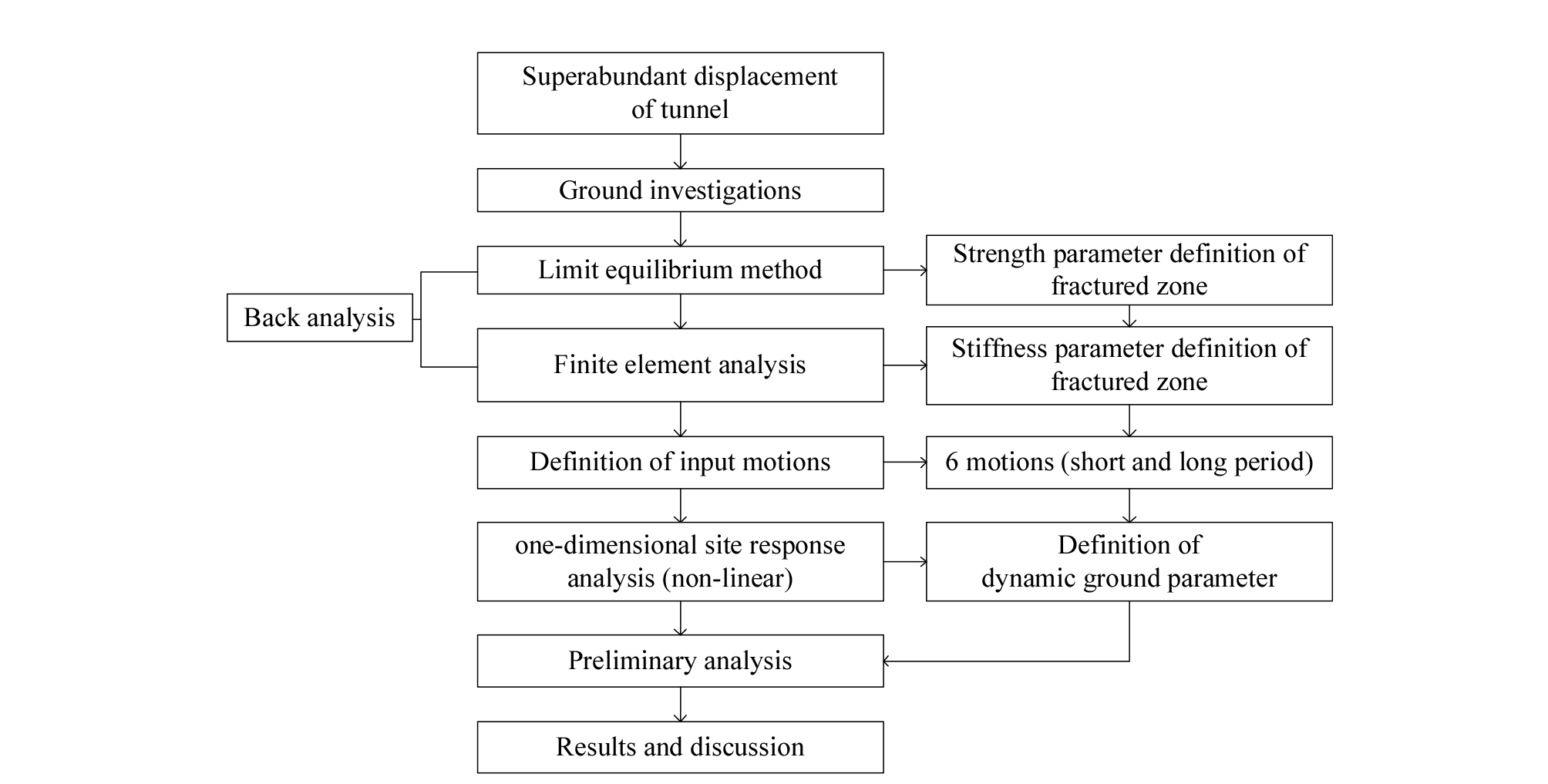
본 연구는 현장에서의 계측결과 및 지반조사 결과와 더불어 수치해석을 통한 역해석, 동적해석, 부지응답해석 등을 통해 수행되었다. 따라서 연구 흐름에 대한 이해를 높이고자 연구 흐름을 Fig. 11에 정리하였다.
3. 결과 및 분석
3.1 터널 단면 거동
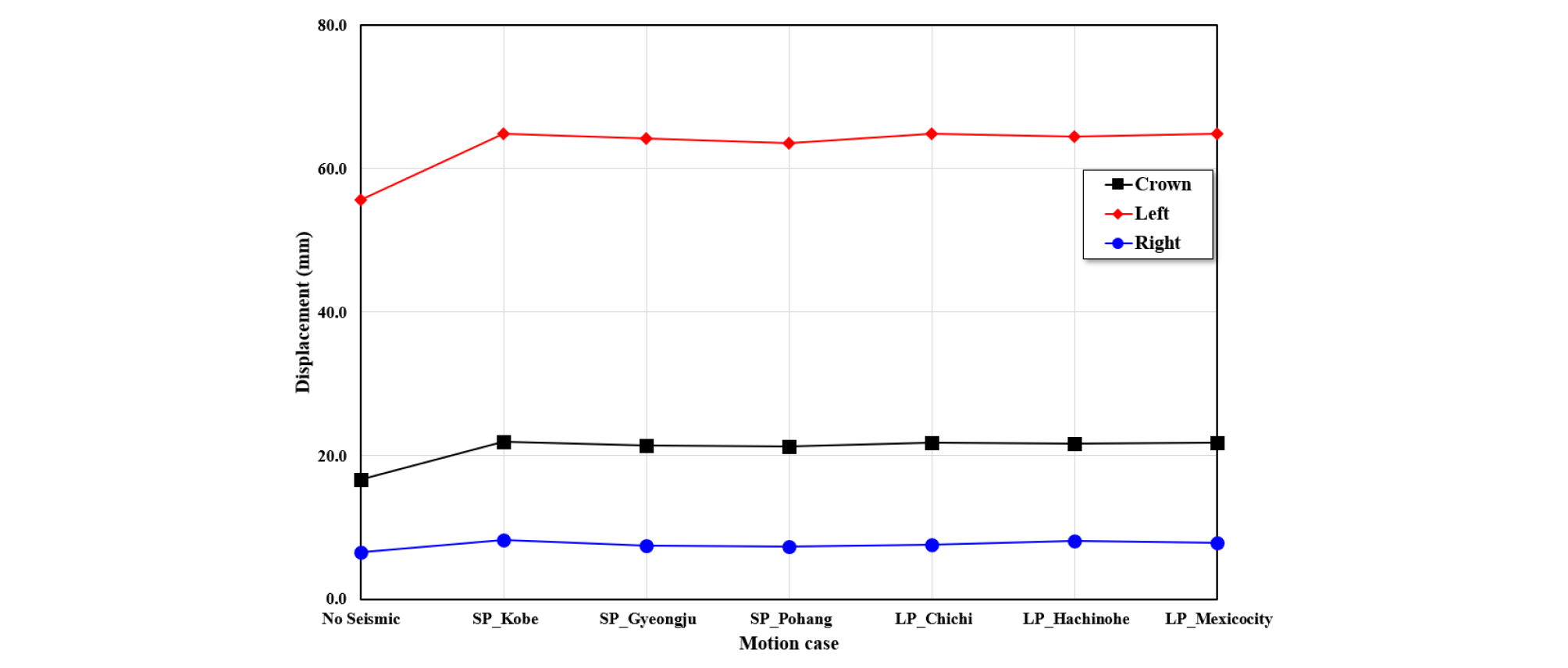
지진하중을 고려한 시공 중 터널의 변위에 대해서 천단변위와 내공변위로 구분하여 나타내었다. 역해석을 통한 천단변위는 지진하중을 고려하지 않았을 경우 16.6 mm로 나타났다. 단주기 지진하중을 고려한 SP_ K (Kobe), G (Gyeongju), P (Pohang)에서 21.9 mm, 21.5 mm, 21.3 mm가 발생하는 것으로 나타났다. 장주기 지진하중이 고려된 LP_C (Chichi), H (Hachinohe), M (Mexicocity)에서는 21.8 mm, 21.7 mm, 21.8 mm가 발생하는 것으로 나타났다. 좌측변위의 경우 현장계측과 동일한 지점에서 발생한 변위는 지진하중이 고려되기 전 55.7 mm가 발생하였으며, 단주기 지진의 경우 SP_K, SP_G, SP_P에서 각각 64.8 mm, 64.2 mm, 63.5 mm의 변위가, 장주기 지진의 경우 LP_C, LP_H, LP_M에서 64.8 mm, 64.4 mm, 64.8 mm가 각각 발생하는 것으로 나타났다. 단층파쇄대의 영향을 덜 받는 우측부는 지진하중이 고려되기 전 6.5 mm로 나타났고 단주기 지진하중에 의해 SP_K, SP_G, SP_P에서 8.2 mm, 7.4 mm, 7.3 mm의 변위가 발생하는 것으로 나타났으며, 장주기 지진에 의해 LP_C, LP_H, LP_M에서 7.6 mm, 8.2 mm, 7.9 mm의 변위가 각각 발생하는 것으로 나타났다(Fig. 12). 그림에서 알 수 있듯이, 주기 특성에 따른 변위차이는 크지 않았다.
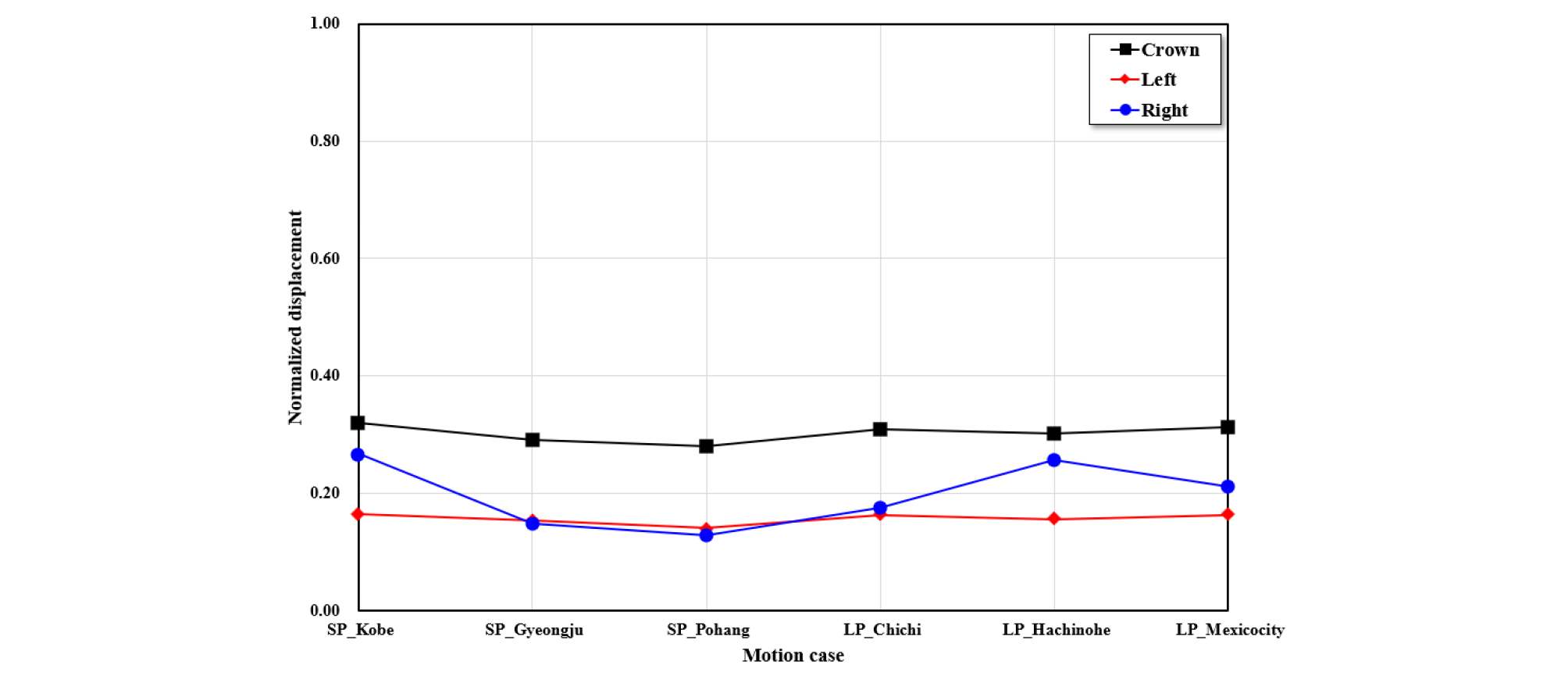
지진하중이 고려되기 전 발생된 터널 단면의 변위 대비 지진하중에 의한 증가량을 정규화하여 Fig. 13에 나타냈다. 단주기 지진하중에 의해 터널의 천단변위는 SP_K, SP_G, SP_P에서 32%, 29%, 28%가량 증가하는 것으로 나타났으며, 장주기 지진하중에 의해서는 LP_C, LP_H, LP_M에서 모두 30~31%가량 증가하는 것으로 나타났다. 단층파쇄대에 의해 과다변위가 발생한 좌측부는 단주기 지진하중에 의해 SP_K, SP_G, SP_P에서 각각 16%, 15%, 14% 증가하는 것으로 각각 나타났으며, 장주기 지진하중에 의해 LP_C, LP_H, LP_M에서 모두 약 16%가량 증가하는 것으로 나타났다. 단층파쇄대의 영향을 받지 않은 우측변위의 경우 단주기 지진하중에 의해 SP_K, SP_G, SP_P에서 각각 27%, 15%, 13% 증가하였으며, 장주기 지진하중에 의해 LP_C, LP_H, LP_M에서 각각 17%, 26%, 21%가량 증가하는 것으로 나타났다. 천단부에서의 증가율이 지진의 주기특성에 관계없이 크게 발생하였으며, 단층파쇄대에 의해 과다변위가 발생된 좌측부의 경우 그 증가율이 다소 작게 나타났다. 이는 좌측부의 인접된 단층파쇄대가 터널 굴착으로 인해 이미 소성상태로 변하여 증가율이 작은 것으로 판단되며, 지진파의 탁월주기가 가장 짧은 포항(SP_P) 및 경주(SP_G)의 경우 천단, 좌측, 우측 모두 변위의 증가율이 미소하지만 가장 작게 발생하였다. 이러한 주기 특성에 따른 시공 중 터널 변위에 대한 연구는 실내모형시험 및 수치해석을 통해 추가 연구가 필요할 것으로 판단된다.
3.2 숏크리트 응력
숏크리트(shotcrete)의 응력을 분석하여 Fig. 14에 나타냈다. 숏크리트에 발생된 응력은 현장계측값과 유사하게 터널의 좌측부와 천단부에서 가장 크게 발생하였다. 천단부에서 지진하중이 고려되지 않았을 경우 447.5 kN의 축력이 발생하였고, 단주기 지진하중에 의해 SP_K, SP_G, SP_P에서 953.6 kN, 962.3 kN, 953.3 kN의 축력이 발생하였고, 장주기 지진하중을 고려하였을 경우 LP_C, LP_H, LP_M에서 954.3 kN, 950.8 kN, 955.5 kN의 축력이 각각 발생하였다. 단층파쇄대에 의한 과다변위 발생지점인 좌측부의 경우 지진하중이 고려되기 전 592.7 kN의 축력이 발생하였으며, 단주기 지진에 의해 SP_K, SP_G, SP_P에서 모두 1,196.6 kN의 축력이 발생하였고 이는 장주기 지진을 고려한 모든 case (LP_C, LP_H, LP_M)에서도 동일하게 나타났다. 우측부 숏크리트의 축력의 경우 지진하중이 고려되지 않았을 경우 178.3 kN의 축력이 발생하였으며, 단주기 지진하중에 의해 SP_K, SP_G, SP_P에서 371.6 kN, 371.8 kN, 369.5 kN의 축력이, 장주기 지진하중을 고려하였을 경우 LP_C, LP_H, LP_M에서 371.9 kN, 368.0 kN, 374.2 kN의 축력이 각각 발생하였다.
대상현장의 숏크리트 관리 기준치 주의(Caution)과 위험(Danger)을 나타냈으며, 지진 발생에 따라 터널의 천단부와 좌측부에서 숏크리트 축력이 기준치를 초과하는 것으로 나타났다.
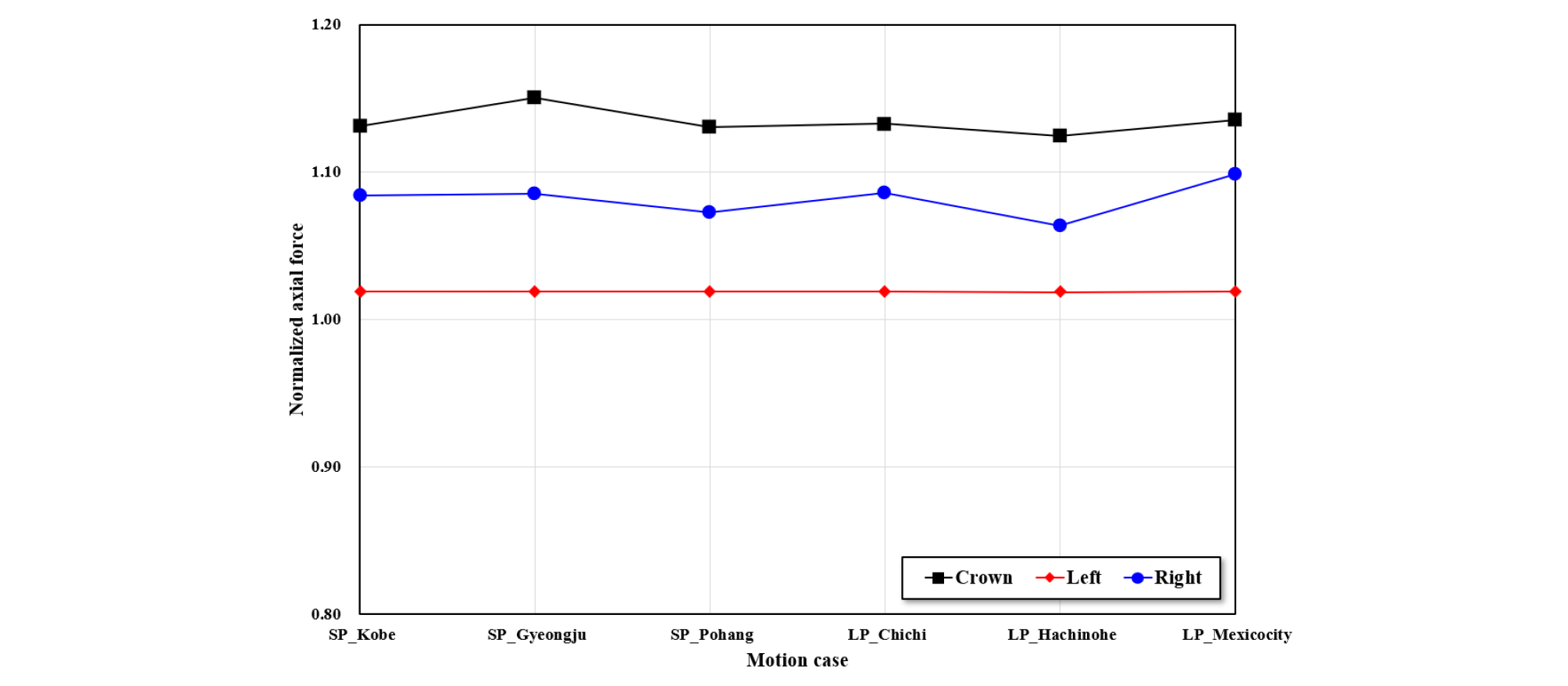
지진하중에 따른 숏크리트 축력의 증가율을 정규화하여 Fig. 15에 나타냈다. 그림에서 알 수 있듯이, 숏크리트 축력의 증가율은 터널의 천단부에서 가장 크게 나타났고(113.1~115.0%) 우측부(106.4~109.8%), 좌측부(106.4~109.8%) 순으로 나타났다. 좌측부의 축력 증가율이 가장 작은 원인은, 앞 절에서 분석한 변위 결과에서 알 수 있듯이, 이미 소성상태로 진행된 단층파쇄대가 지진하중에 의해 변위는 발생하였지만, 숏크리트가 단층파쇄대에 저항할 수 없는 것을 의미한다.
3.3 록볼트
3.3.1 변위
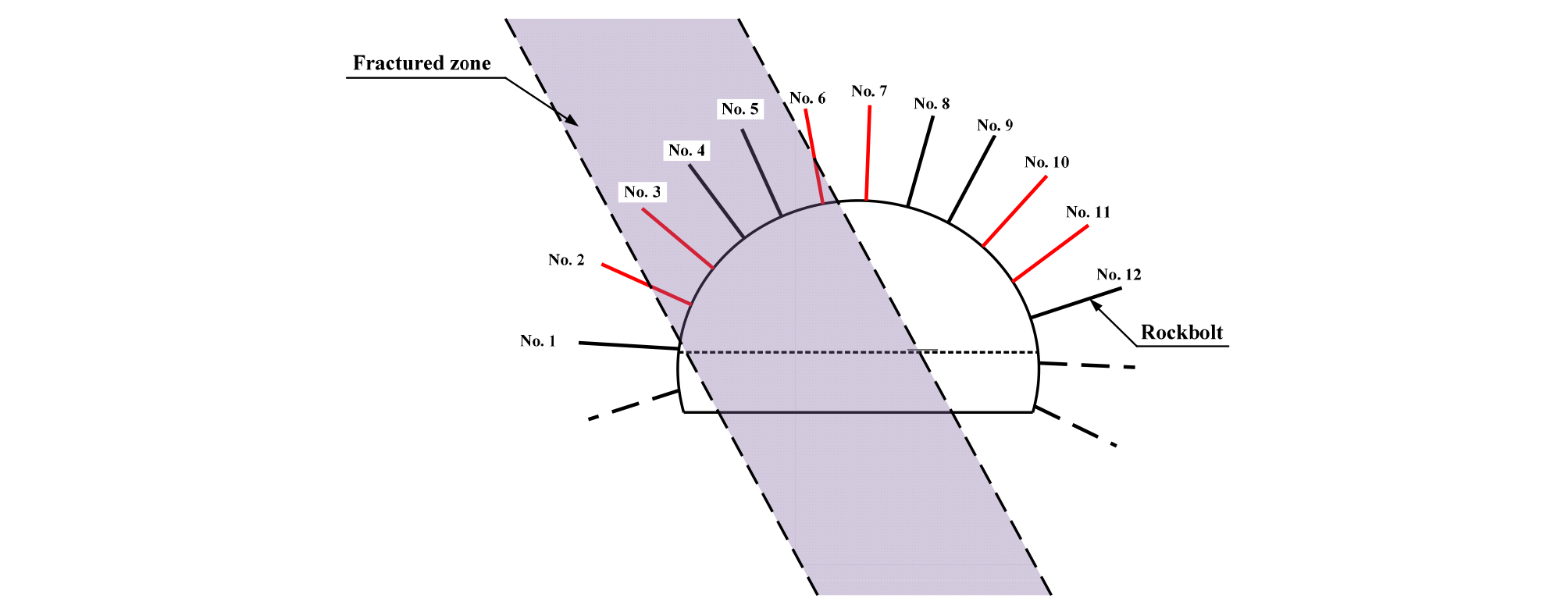
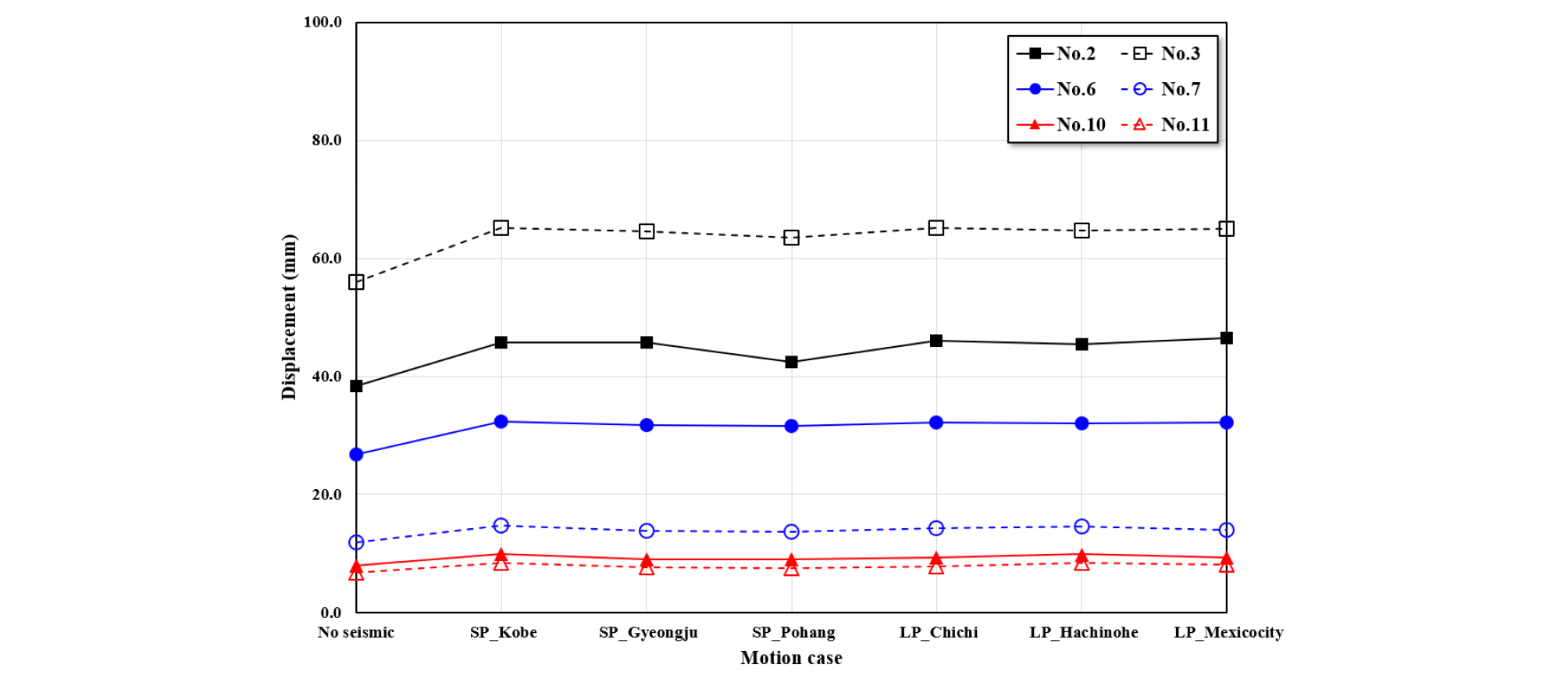
록볼트(Rockbolt)를 위치별로 분석하기 위해 좌측부부터 No. 1~No. 12로 지정하였다(Fig. 16). 좌측부에서는 No. 2, 3를 선정하였으며 천단부에서는 No, 6, 7를, 우측부에서는 No. 10, 11의 결과를 분석하였다. 좌측부 및 천단부의 경우 기반암과 단층파쇄대에 정착되어 있는 록볼트를 각각 선정하였으며, 우측부는 좌측부와 동일한 위치에 설치된 록볼트를 선정하여 변위를 분석하였다(Fig. 17).
No. 2에서 발생된 록볼트의 변위는 지진하중이 고려되기 전 38.4 mm의 변위가 발생하였으며, SP_K, SP_G에서 45.7 mm, SP_P에서는 42.4 mm의 변위가 나타났고, LP_C, LP_H, LP_M에서 46.0 mm, 45.4 mm, 46.6 mm의 변위가 나타났다. 단층파쇄대에 설치된 No. 3의 경우 지진하중이 고려되기 전 55.9 mm의 변위가 발생하였으며, 63.5~65.2 mm의 변위가 단주기 지진에 의해 발생하였다. 장주기 지진이 고려된 경우 64.7~65.2 mm의 변위가 발생하였다.
천단부에서 단층파쇄대와 기반암에 설치된 No. 6의 경우, 지진하중이 고려되지 않았을 때 26.7 mm의 변위가 발생하였고, 단주기 지진 및 장주기 지진에 의해 31.5~32.4 mm의 변위가 발생하는 것으로 나타났다. No. 7의 경우 지진하중이 고려되기 전 11.9 mm의 변위가, 단주기 및 장주기 지진에 의해 13.7~14.7 mm의 변위가 발생하였다.
우측부의 경우 좌측부와 천단부에 비해 그 변위량이 작게 나타났다. No. 3과 대응되는 No. 10의 경우 지진하중이 고려되기 전 8.0 mm, 단주기 및 장주기 지진에 의해 8.9~9.9 mm의 변위가 발생하였고, No. 11의 경우 지진하중이 고려되지 않았을 때 6.7 mm, 지진하중에 의해 7.5~8.4 mm의 변위가 발생하였다.
천단부 및 좌측부에서 록볼트의 정착지반이 단층파쇄대+기반암인 No. 2와 6에서 변위가 기반암에만 정착된 No. 3과 7 보다 크게 발생되는 것으로 나타났는데, 이는 다음 절에서 분석된 록볼트의 축력 결과와 유사한 것으로 나타났다. 이러한 록볼트의 변위는 록볼트의 축력에 영향을 미치는 요소로써 단층파쇄대로 인한 편토압으로 인해 발생되는 것이라 할 수 있다.
또한 우측부 No. 10, 11은 기반암에만 정착되어 있지만 No. 3, 7과는 큰 변위차이를 보였으며, 이는 단층파쇄대에 인접한 지반에 의한 것으로 판단되었다.
3.3.2 축력
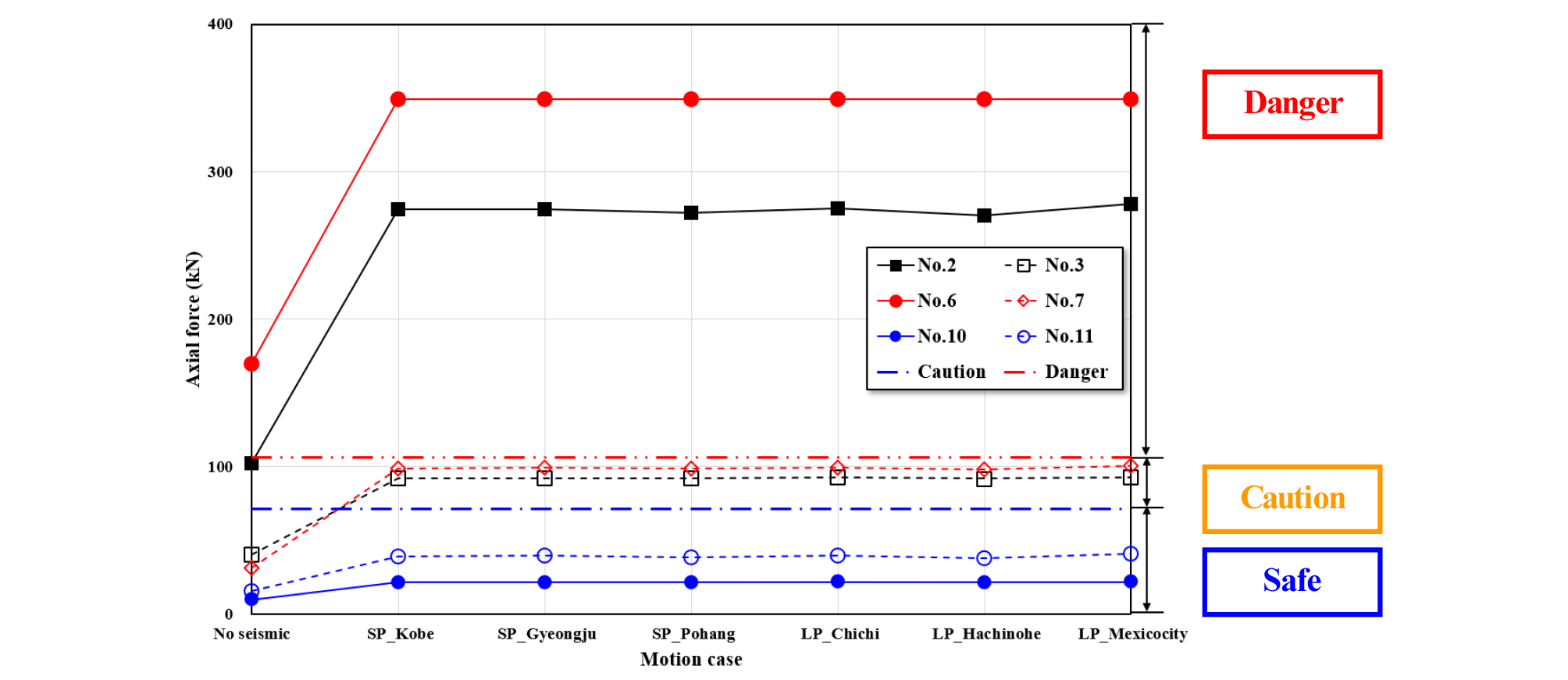
록볼트에 발생되는 축력을 분석한 결과를 Fig. 18에 나타냈다. 지진하중이 고려되기 전 No. 2에 작용하는 축력은 102 kN, 단주기 및 장주기 지진에 의해 발생된 축력은 207.6~277.9 kN로 나타났다. No. 3의 경우 지진하중이 고려되기 전 40.3 kN의 축력이 발생하였으며, 단주기 및 장주기 지진하중에 의해 91.7~92.8 kN의 축력이 발생하였다.
천단부에 위치한 No. 6의 경우 지진하중이 적용되지 않았을 때 169.6 kN, 지진하중에 의해 349.0~349.3 kN의 축력이 발생하였고, No. 7에서는 지진하중 고려 전 31.0 kN, 지진하중 고려 후 98.2~100.3 kN의 축력이 발생하는 것으로 나타났다.
우측부의 No. 10의 경우 지진하중이 고려되지 않았을 때 9.7 kN의 축력이 발생하였으며, 단주기 및 장주기 지진하중에 의해 21.4~21.7 kN의 축력이 발생하였다. No. 11의 경우 지진하중 발생 전 15.5 kN의 축력이, 지진하중 발생 후 37.6~40.6 kN의 축력이 발생하는 것으로 나타났다.
Fig. 18에는 각각의 case에서 발생한 록볼트의 축력을 관리 기준치와 함께 나타냈다. 1점 쇄선은 주의, 2점 쇄선은 위험을 의미하며, 단층파쇄대와 기반암에 동시에 정착되어 있는 No. 2, 6의 축력이 가장 크게 나타났다. 또한 단층파쇄대에 정착되어 있는 No. 3의 경우 록볼트의 증가율이 No. 2, 6에 비해 작게 나타났는데 이는 단층파쇄대가 이미 소성상태가 되어 변위가 크게 발생하여 록볼트가 정착이 무의미해져 나타나는 것으로 판단된다. 반면, 단층파쇄대와 인접하지 않은 No. 10, 11의 경우 지진하중에 의해 약 120~150%가량 축력이 증가하는 것으로 나타났다. 지진하중의 주기특성에 따른 축력의 차이는 매우 미미하게 나타났는데 이는 록볼트 길이가 4 m로 적용되어 주기특성이 나타나기에는 그 길이가 매우 짧은 것이 원인으로 판단된다. 따라서 본 연구를 기초로 록볼트의 길이, 지진 주기특성 및 가속도의 조건을 달리하여 실내모형시험 및 수치해석을 통한 추가 연구가 필요할 것으로 판단된다.
4. 결 론
본 연구에서는 터널 시공 중 단층파쇄대에 의해 과다변위가 발생된 대상 현장의 단면의 변위, 숏크리트 및 록볼트의 축력 계측값을 기준으로 역해석을 수행하였다. 이후 지진하중을 고려하여 지진하중에 의한 시공 중 터널의 거동을 수치해석을 통해 분석하였다. 단층파쇄대의 물성치는 한계평형해석과 유한요소해석을 통해 산정하였다.
지진하중은 지진의 주기 특성을 고려하여 단주기 지진과 장주기 지진으로 구분하였으며, 가속도는 재현주기 1000년으로 0.154 g로 scalling하여 적용하였다.
터널의 좌측부 변위의 경우 단층파쇄대의 영향으로 인해 지진하중 고려 전 가장 큰 변위가 발생하였지만, 지진하중에 의한 변위증가량은 가장 적게 나타났으며, 단층파쇄대와 인접해 있는 천단부의 경우 지진하중에 의해 가장 큰 추가변위가 발생하는 것을 알 수 있었다. 우측부의 경우 단주기 지진에 비해 장주기 지진에서 다소 큰 변위 증가량을 보였으나 그 차이는 미미하였으며, 전체적으로 터널의 천단, 좌측 및 우측부에서 약 15~35%가량 변위가 증가하는 것으로 나타났다.
숏크리트에 발생된 축력의 경우 천단부에서는 지진하중에 의해 약 113.0~115.0%가 증가하였고 우측부에서는 106.4~109.8%, 좌측부에서는 101.9% 증가하는 것으로 나타났다. 단층파쇄대의 영향을 가장 많이 받는 좌측부에서 숏크리트 축력의 증가율이 가장 작은 이유는 단층파쇄대가 소성상태로 전이되어 숏크리트가 인접지반의 토압에 저항하지 못하는 상태가 원인인 것으로 판단된다.
단층파쇄대와 인접하지 않은 우측부의 숏크리트 축력은 지진하중 고려 이후에도 안전영역에 있었지만, 단층파쇄대와 인접한 천단부의 경우 지진하중에 의해 안전영역에서 주의영역에 도달하였으며, 위험기준에 근접하게 증가하는 것을 알 수 있었다.
록볼트의 거동은 변위와 축력으로 구분하여 분석하였으며, 단층파쇄대와 인접한 천단부와 좌측부의 경우 기반암과 단층파쇄대에 동시에 정착된 록볼트와 기반암 또는 단층파쇄대에만 정착된 록볼트, 우측부는 좌측부와 동일한 높이에서의 록볼트를 선정하여 분석하였다.
지진하중에 의해 발생된 록볼트의 변위는 좌측부에서 가장 크게 발생하였으며, 천단부, 우측부 순으로 나타났다. 뿐만 아니라, 좌측부와 천단부에서 단층파쇄대와 기반암에 동시에 정착된 록볼트의 변위가 크게 나타났으며 이는 록볼트의 축력 변화에 영향을 미치는 것을 알 수 있었다. 록볼트의 변위는 지진하중에 의해 전체적으로 약 13.0~25.0%가량 증가하는 것으로 나타났다.
지진하중을 고려한 수치해석 결과를 현장의 계측기준치와 비교하였다. 좌측부와 천단부에서 단층파쇄대와 기반암에 동시에 정착되어 있는 록볼트의 축력이 크게 영향을 받는 것으로 나타났으며, 그 증가율은 약 100~150%로 나타났다. 우측부의 경우 또한 지진하중에 의하 120~150%의 축력이 증가하는 것으로 나타났다. 천단부의 경우는 좌측부 및 우측부의 록볼트 보다 축력 증가율이 110~210%로 더 크게 나타났으며, 이는 단층파쇄대로 인해 발생되는 토압의 수직분력이 수평분력보다 큰 이유인 것으로 판단된다.
본 연구는 다양한 가정조건에서 수치해석을 통해 수행된 연구로서, 실제 설계 및 시공단계에서 사용할 수 있는 연구결과 도출을 위해서는 추가 연구가 필요할 것으로 판단된다. 다만, 시공 중 터널에 설치된 록볼트의 경우 동일한 지반에 정착된 경우보다 다층지반에 정착된 경우 지진발생 후 보다 세밀한 관리 및 계측이 필요할 것으로 판단된다.