1. 서 론
2. 동적해석기법 비교
2.1 유한요소법(MIDAS GTS NX)
2.2 유한차분법(FLAC 2D)
3. 동적해석 모델링
4. 해석 기법별 결과 비교
4.1 수평변위
4.2 가속도 이력 및 층간변위비
4.3 초고층 건물의 휨응력 및 취약부
5. 결 론
1. 서 론
최근 경주, 포항뿐만 아니라 우리나라 전 지역에서 지진이 발생하고 이에 건축 및 모든 분야에서 많은 내진연구 및 해석이 수행되고 있다. 일반적으로 지반-구조물 상호작용(Soil-Structure Interaction, SSI)을 고려한 동적해석 시 적용 가능한 수치해석 방법의 종류에는 유한요소법과 유한차분법, 경계요소법 등이 있다. 국내 실무에서 많이 사용되는 지반 범용 해석프로그램으로는 유한요소법에 기초를 둔 MIDAS GTS NX와 유한차분법에 기초를 둔 FLAC 프로그램이 있다.
Hwang (2000)은 풍화암, 연암, 경암에 위치한 4개 터널 현장에서 13개 단면을 선정하여 유한차분(FLAC 2D)과 유한요소(SMAP)해석을 수행하고 측압계수 변화에 따른 천단변위, 지보재 응력 등을 상호 비교 ‧ 분석하였다. 측압계수가 증가할수록 지표침하, 천단 및 인버트변위는 유한차분해석보다 유한요소해석이, 내공변위와 지보재 압축응력은 유한요소해석보다 유한차분해석이 더 보수적인 결과를 준다고 주장하였다. 그러나 해석 대상을 터널에 한정하였고, 동적해석을 수행하지 않았기 때문에 동적거동에 대한 두 해석방법의 차이를 비교 ‧ 분석하지 않았다.
초고층 건물에 인접한 지하구조물이 초고층 건물에 미치는 영향을 분석하고자 You and Kim (2018)은 구조물 높이, 인접지하구조물의 유 ‧ 무, 지진파 크기(PGA)를 파라미터로 지반 범용 프로그램인 FLAC 2D를 사용하여 SSI를 고려한 동적해석을 실시하고, 각 파라미터에 대해 민감도 분석을 수행하였다. 그 결과, PGA, 구조물의 높이, 인접지하구조물 유 ‧ 무에 관계없이 초고층 건물의 층간변위비는 ‘즉시기준’ 수준 이내로 발생하였으나 초고층 건물 지하부 3층 좌 ‧ 우측 벽체의 휨인장응력은 허용 휨인장응력을 초과하여 취약부인 것으로 나타났다. 따라서 초고층 건물의 동적안정성 평가 시 인접지하구조물의 영향을 고려하는 것이 필요하다고 주장하였지만 수치해석 기법에 따른 초고층 건물의 SSI 동적안정성 평가를 수행하지 않았다.
도심지 터널 발파 시 발생하는 발파진동의 영향권을 분석하기 위하여 Son (2012)은 도시철도 2호선 ○○○공구 건설공사 구간을 대상으로 얻어진 발파진동 계측 데이터를 활용하였다. 이를 위해 발파 시 발생하는 발파 진동을 MIDAS GTS NX를 이용하여 구하고, 현장 계측치와 비교 ‧ 분석하였다. 각 지점별 실제 발파 진동데이터와 수치해석 결과는 최대 오차가 22%로 나타나 유사하게 산출되었지만, 진동값이 규제기준치를 초과한 것으로 나타났다.
구조물과 지반의 거동을 파악하기 위해 국내에서 자주 이용되는 지반 범용 프로그램은 유한요소법과 유한차분법에 각각 기초한 MIDAS GTS NX와 FLAC 2D이다. 근본적으로 MIDAS GTS NX의 경우는 선형시간이력해석 중 모드중첩법이나 직접적분법을, FLAC 2D는 직접적분법만을 이용하여 운동방정식의 해를 구한다. MIDAS GTS NX의 경우는 대상 전체 시스템에 대해 고유치해석을 수행하여 질량참여율이 높은 1, 2차 모드의 고유주기를 구하고 각 모드별 감쇠비를 입력하여 질량강성계수를 계산하거나, 직접 질량강성계수를 입력하여 동적해석을 수행한다. 반면, FLAC 2D는 건물과 지반 각각의 고유주기와 감쇠비를 문헌을 참고하거나 추정식을 이용하여 산정하고 동적해석을 수행한다. 한편, MIDAS GTS NX 프로그램은 실무에서 동적해석을 위해 널리 사용되지만 신뢰성 검증을 위해 비교 ‧ 분석이 필요하다.
본 연구는 수치해석 기법의 따른 두 프로그램의 SSI 동적해석에 대한 신뢰성을 검증하고자 하였다. 이를 위해 동일한 해석 파라미터인 대상건물, 지반조건, 지진파 특성을 사용하여 각 프로그램별로 SSI 동적해석을 수행하고 결과를 비교 ‧ 분석하였다. 대상구조물은 초고층 건물과 그에 인접한 지하구조물로 각각 높이 275 m, 55층, 층고 5 m, 지하 4층, 25 m로, 높이 15 m, 층고 5 m, 지하 3층으로 구성되는 것으로 하였다. 입력지진파로는 재현주기 1,000, 2,400년에 해당하는 최대지반가속도(PGA)인 0.154 g, 0.22 g의 1968년 일본에서 발생한 Hachinohe 지진파를 사용하여 유한요소법(MIDAS GTS NX)과 유한차분법(FLAC 2D)에 의해 선형시간이력해석(직접적분법)을 수행하고, 초고층 건물의 수평변위, 층간변위비, 구조부재에 작용하는 휨응력, 취약부 위치를 비교 ‧ 분석하였다.
2. 동적해석기법 비교
2.1 유한요소법(MIDAS GTS NX)
유한요소 해석법(Finite Element Method, FEM)에 근거를 지반-구조물 상호거동에 대한 상세해석을 위해 개발된 대표적인 프로그램으로 MIDAS GTS NX가 있다. 유한요소법은 미분방정식의 해를 계산하는 수치해석 근사해법으로, 미분방정식을 연립대수 방정식으로 변환하여 운동방정식을 구하게 되는데, 이를 위해 모드중첩법(Mode Superposition Method)이나 직접적분법(Direct Integration Method)을 이용된다. 모드중첩법이란 각 모드별로 해석을 수행하여 응답을 더하는 방법으로, 제한된 자유진동모드만을 사용하여 대형 구조물의 동적 거동을 정확하게 나타낼 수 있을 때 효과적으로 사용할 수 있다(Kim, 2013). 반면에 직접적분법은 전체 해석영역의 자유도를 미지수로 하는 시간이력해석으로, 전체 자유도에 대한 동적 평형방정식을 시간에 따라 점진적으로 적분하여 해를 구하는 방법이다. 또한, 모든 시간단계에 대하여 해석을 수행하기 때문에 시간 단계의 수에 비례하여 해석시간이 소요된다(MIDAS Information Technology Co., 2016).
모드중첩법의 경우 각 모드별로 사용자가 직접 감쇠비를 입력하게 되고 정의된 모드별 감쇠비에 따라 응답을 계산한다. 또한, Rayleigh의 감쇠행렬인 C=𝛼M+𝛽K식의 질량강성계수 𝛼, 𝛽를 직접 계산하여 입력하거나 고유치해석을 통하여 계산된 고유주기와 각 모드의 감쇠비를 입력하게 된다. 직접적분법 감쇠의 경우 모드별 감쇠를 제외한 Rayleigh의 감쇠행렬의 질량강성계수 𝛼, 𝛽를 직접입력하거나, 고유주기와 각 모드의 감쇠비를 입력한다. 경계조건으로는 탄성, 점성경계를 적용하여 지진파가 해석 경계면에서 흡수되어 반사되는 현상을 방지한다(MIDAS Information Technology Co., 2012).
2.2 유한차분법(FLAC 2D)
유한차분법에 근거한 대표적인 수치해석 프로그램으로 FLAC (Fast Lagrangian Analysis of continua) 2D가 있다. 지반 및 구조물을 각 절점에 연결된 요소인 연속체로 간주한다는 점에서 유한요소법과 유사하나 미지수를 구하는 방법에 대해 차이점이 있다. FLAC 2D는 운동방정식의 해를 구하기 위해 직접 적분값을 구하는 방법인 직접적분법을 이용한다. MIDAS Information Technology Co. (2016)에서는 시간이력해석 중 직접적분법과 모드중첩법에 대한 동적해석 특성의 일반적인 사항을 Table 1과 같이 정리하였다. MIDAS GTS NX는 모드중첩법이나 직접적분법을, 반면에 FLAC 2D의 경우는 직접적분법만을 적용하여 시스템방정식의 해를 구할 수 있다. 하지만 MIDAS GTS NX와 FLAC 2D 프로그램 모두 동적감쇠를 위해 질량 강성-비례감쇠법(Mass, stiffness- proportional damping)인 Rayleigh 감쇠 등이 사용될 수 있다.
Table 1. The comparison between two commercial programs in terms of dynamic analysis characteristics
FLAC 2D에서는 고유치 해석을 수행하지 않고, 구조물과 지반의 고유주기를 구분하고, 추정식을 통해 계산하거나 문헌을 통해 각각 산정하여 입력하게 된다. 한편 감쇠는 Rayleigh damping, Hysteretic damping 등이 사용될 수 있다. 경계조건으로는 요소망의 측면경계에서 지진파가 반사되어 해석결과에 영향을 미치는 것을 막기 위해 해석영역의 좌, 우측 경계는 자유장 경계(free-field boundary)를 적용한다. 그리고 deconvolution을 수행하여 지진파의 진동이 과대평가되는 것을 막기 위해 요소망의 하부경계에 quiet 경계(점성댐퍼)를 적용한다(You and Kim, 2018).
3. 동적해석 모델링
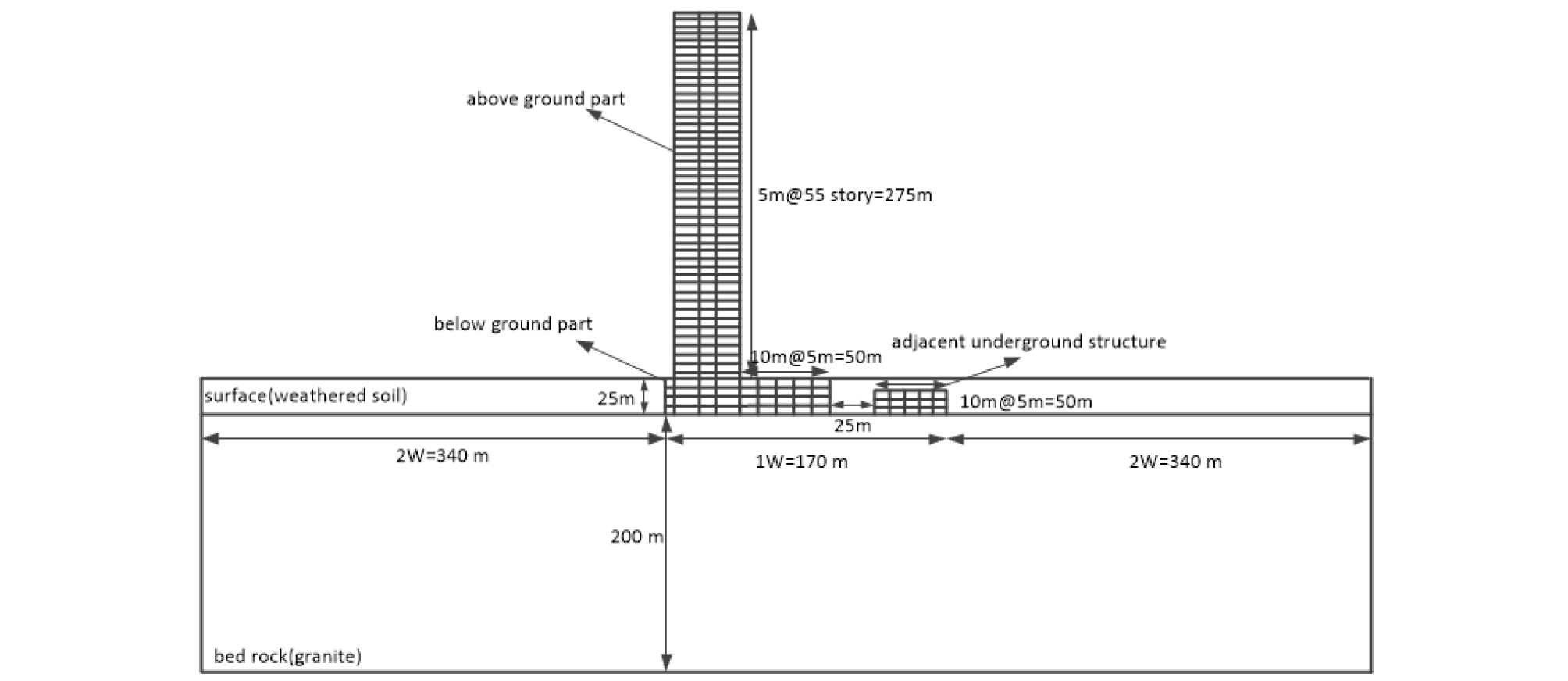
본 연구에서는 유한요소법에 근거한 MIDAS GTS NX 프로그램과 유한차분법에 기초한 FLAC 2D 프로그램을 이용하여 Fig. 1과 같이 SSI를 고려한 초고층 건물(55층, 지하 5층), 인접지하구조물(지하 3층)을 대상으로 동적해석을 수행하였다. 초고층 건물과 인접지하구조물은 기반암인 화강암 위에 설치되어 있는 것으로 하고, 지표면으로부터 25 m 깊이로 풍화토가 존재하여 초고층 건물의 지하부와 인접지하구조물은 풍화토 내에 시공되도록 하였다. 초고층 건물의 지상부는 55층(총 건물 높이 275 m, 층고 5 m)으로 하였으며, 내부 기둥은 9 m 간격으로 2개를 모사하였다. 건물 좌 ‧ 우측 벽체는 기둥으로부터 12.6 m 이격시켜 적용하였다. 지상부와 연결된 지하부 기둥의 경우 지상부와 동일한 간격으로 하고 그 외의 지하부 기둥은 10 m 간격으로 설치하였다. 또한 지하부의 층고는 지하 1층부터 각각 7.5 m, 6.0 m, 8.0 m, 3.5 m로, 인접지하구조물의 경우 3층(층고 5 m)이고 기둥 간격이 10 m인 폭 50 m로 적용하였다. 또한 지표면으로 10 m 아래에 인접지하구조물의 천정부가 설치되어 있는 것으로 모사하였다.
해석영역은 초고층 건물의 좌측 지하벽체로부터 인접지하구조물 우측벽체까지의 거리(170 m)를 기준으로 2배에 해당하는 340 m를 각각 좌 ‧ 우로, 초고층 건물의 지하부 바닥면으로부터 약 1.2배인 200 m를 하부로 확대하여 설정하였다. 또한 MIDAS GTS NX와 FLAC 2D 모두 대상 건물과 지반의 요소 크기는 가능하면 2 m × 2 m가 되도록 하였다. 결과적으로 MIDAS GTS NX의 경우 요소수는 초고층 건물 636개, 인접지하구조물 136개, 지반 46,358개로, FLAC 2D의 경우는 초고층 건물 645개, 인접지하구조물 124개, 지반 42,770개로 요소수를 비슷하게 하였다.
본 해석에 적용한 표층과 기반암은 각각 풍화토와 화강암을 적용하였으며 물성치는 ○○ 설계회사가 실시설계에 사용한 자료(Western Metro, 2016)를 참고하여 Table 2와 같이 적용하였다. 그리고 측압계수는 표층과 기반암 모두 1.0을 적용하였으며, 지반구성 모델로 Mohr-Coulomb 파괴기준을 적용하였다. 한편, 동일한 재료나 서로 다른 재료간의 접촉을 모사하기 위해 경계요소(interface element)를 고려해야하나, 본 연구에서는 지반과 구조물이 일체로 거동하는 것으로 가정하여 고려하지 않았다.
Table 2. Ground properties
| Ground type |
Unit weight (kN/m3) |
Elastic modulus (MPa) | Poisson's ratio | Friction angle (˚) | Cohesion (kPa) |
|
Weathered soil (surface) | 19 | 25 | 0.32 | 29 | 20 |
|
Granite (bed rock) | 26 | 15,000 | 0.22 | 43 | 2,500 |
동적해석에 적용된 초고층 건물과 인접지하구조물은 beam 요소를 사용하여 슬래브, 벽체 그리고 기둥으로 모사되었으며, 각각에 대한 물성치는 Table 3과 같다. 유한차분법의 FLAC 2D 프로그램 적용 시 구조물 부재별로 파괴를 고려하기 위해 Table 3과 같이 소성모멘트(plastic moment)를 적용하였다. 이는 두께가 0.35 m, 철근의 직경과 유효깊이가 각각 25 mm와 240 mm이고 하단에 단위 미터 당 3개가 배근되어 있는 단면을 가정하여 산정한 것이다. 반면 MIDAS GTS NX 프로그램 적용 시는 소성모멘트를 입력할 수 없어서 부재의 파괴는 고려되지 않았다. 또한 유한요소법(MIDAS GTS NX)과 유한차분법(FLAC 2D)에 의한 해석 모두 구조물의 자중을 고려하기 위해 철근콘크리트의 단위중량을 25 kN/m3으로 적용하였으며 그 외의 활하중 및 사하중은 각각 4.2 kN/m2, 2.5 kN/m2으로 가정하여 슬래브 1 m2당 6.7 kN의 하중을 가하였다.
Table 3. Properties of building structural members
본 연구에서는 초고층 건물과 인접지하구조물이 RC 구조물로 시공되었다고 가정하였다. 따라서 콘크리트 표준시방서(Ministry of Land, Infrastructure and Transport, 2016)에서 제시한 고강도 콘크리트의 설계기준강도(𝜎ck)가 40.0 MPa인 것을 참고하여 허용 휨압축, 인장 및 전단응력을 각각 24.0, 4.0, 2.4 MPa로 적용하였다(You et al., 2005).
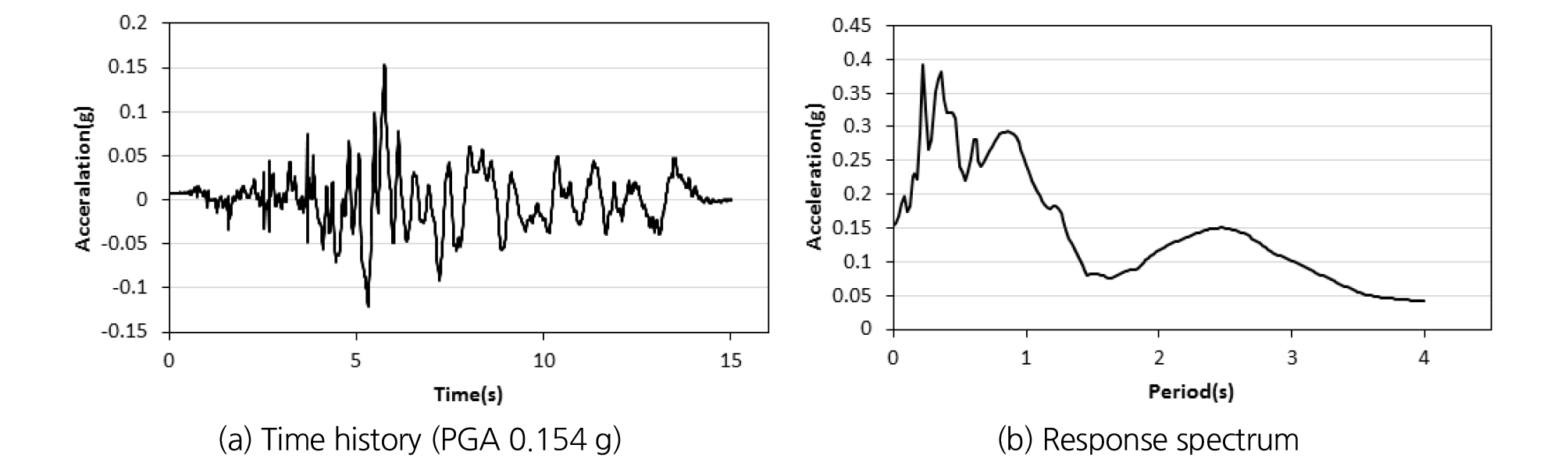
입력지진파는 Fig. 2(a)와 같이 가진 시간이 15초이고 탁월주기는 0.5초(탁월주파수는 2 Hz) 장주기파인 Hachinohe파를 적용하였다. Fig. 2는 0.154 g를 예시로 가속도 이력과 가속도 응답스펙트럼을 보여준다. Fig. 2(b)로부터 탁월주기가 짧은 0.2초뿐만 아니라, 긴 2.5초에서도 나타나는 장주기파임을 알 수 있다.
MIDAS GTS NX를 이용한 선형시간이력해석(직접적분법)을 수행하기 위해서는 Rayleigh 질량강성계수를 정해야 된다. 이를 위해 건물과 지반의 전체시스템에 대한 고유치 해석을 통하여 산정된 질량참여율이 높은 1, 2차 모드의 고유주기와 각 모드의 감쇠비를 각각 0.05를 입력하였다. 한편 FLAC 2D의 경우 Rayleigh 감쇠에 의하여 초고층 건물의 감쇠비와 주파수를 각각 0.008과 0.2를 적용하였고, 지반의 감쇠비는 0.05와 4.5를 적용하였다(Park et al., 2015; Itasca Consulting Group, Inc., 2005; Koo and Kim, 2015). MIDAS GTS NX의 경우 고유치해석을 수행하여 고유주기를 전체 영역인 지반과 건물의 고유주기 6.4초(1차 모드), 1.4초(2차 모드)를 산정하였다. 고유치해석을 수행하기 위해 식 (1)을 적용하여 지반반력계수(Kv)를 구하고 기반암, 표층 좌 ‧ 우측에 산정된 지반반력계수를 입력하고, 탄성경계를 적용하여 지반반력이 모사되도록 하였다.
| $$K_v=K_{v0}\times(B_v/0.3)^{-3/4}(\mathrm{kN}/\mathrm m^3)$$ | (1) |
여기서, (kN/m3), E0 = 탄성계수(kN/m2)이다.
또한 MIDAS GTS NX는 지진파가 경계에 흡수되기 위하여 Lysmer and Kuhlemeyer (1969)가 제안한 점성경계조건을 기반암 바닥, 기반암, 표층 좌 ‧ 우측에 각각 식 (2)와 식 (3)을 적용하여 점성경계계수(Cp, Cs)를 구하고 점성경계조건을 적용하였다. 반면, FLAC 2D의 경우 측면경계에서 지진파가 반사되는 것을 막기 위해 해석영역의 좌 ‧ 우측은 자유장 경계를 적용하였다. 또한 기반면의 하부에 지진파를 가진시키기 위해 요소망 하부의 수직, 수평방향의 변위를 구속하였다.
| $$C_p=\rho A\sqrt{\frac{\lambda+2G}\rho}$$ | (2) |
| $$C_s=\rho A\sqrt{\frac G\rho}$$ | (3) |
여기서, 𝜆는 , G는 , 𝜌는 밀도, A는 적용 면적이다.
4. 해석 기법별 결과 비교
4.1 수평변위
초고층 건물과 인접지하구조물에 대한 동적해석 시 지상 건물의 수평변위를 건물의 좌측 벽체를 기준으로 산출하여 유한요소법(MIDAS GTS NX)과 유한차분법(FLAC 2D)에 의해 수행된 결과를 비교 ‧ 분석하였다. Table 4는 두 프로그램에 따른 초고층 건물의 최대 수평변위를 가진 시간 4초, 8초, 12초, 16초에서 발생한 건물의 층수를 나타낸 것이다.
Table 4. The comparison of the maximum horizontal displacement of a high-rise building (PGA = 0.154 g)
초고층 건물의 최대 수평변위가 발생한 가진 시간은 MIDAS GTS NX와 FLAC 2D 모두 12초로 나타났고 MIDAS GTS NX의 경우 최대 수평변위는 88.04 cm가 발생하였다. FLAC 2D의 최대 수평변위는 94.67 cm가 초고층 건물 최상단에서 발생하여 두 해석프로그램의 결과값이 유사함을 알 수 있었다. 각 가진 시간에 두 프로그램으로 산출된 최대 수평변위의 차이는 약 3.7 cm로 미세한 차이가 산출되었다. 또한 가진시간별 최대 수평변위 발생 위치도 동일하게 나와 MIDAS GTS NX와 FLAC 2D의 유사성을 확인하였다.
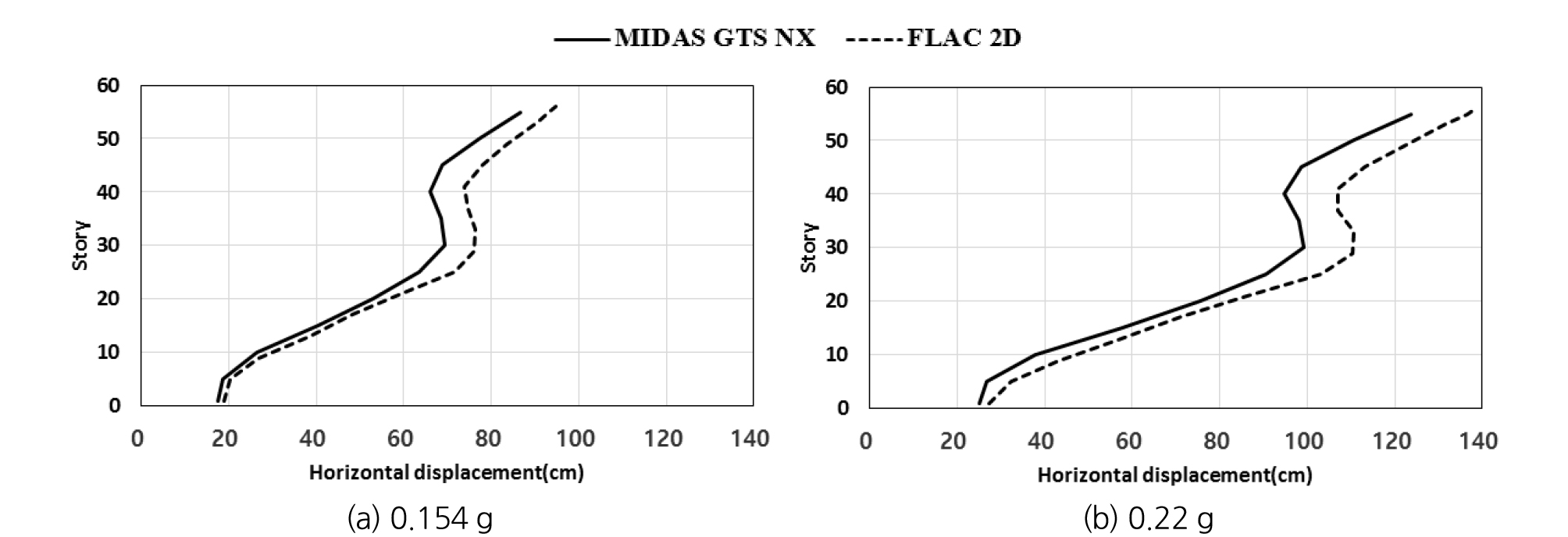
Fig. 3은 수치해석 프로그램에 따른 PGA 0.154 g, 0.22 g가 작용할 경우 초고층 건물 좌측 벽체를 기준으로 수평변위분포를 나타낸 것이다. 최대 수평변위는 초고층 건물 최상단에서 동일하게 발생하였다. 한편, MIDAS GTS NX와 FLAC 2D의 수평변위분포 값의 차이는 0.154 g의 경우 약 2~10 cm, 0.22 g의 경우는 약 3~15 cm 정도 발생하였다. 반면 수평변위분포 양상은 MIDAS GTS NX와 FLAC 2D 모두 유사하게 나타났다.
4.2 가속도 이력 및 층간변위비
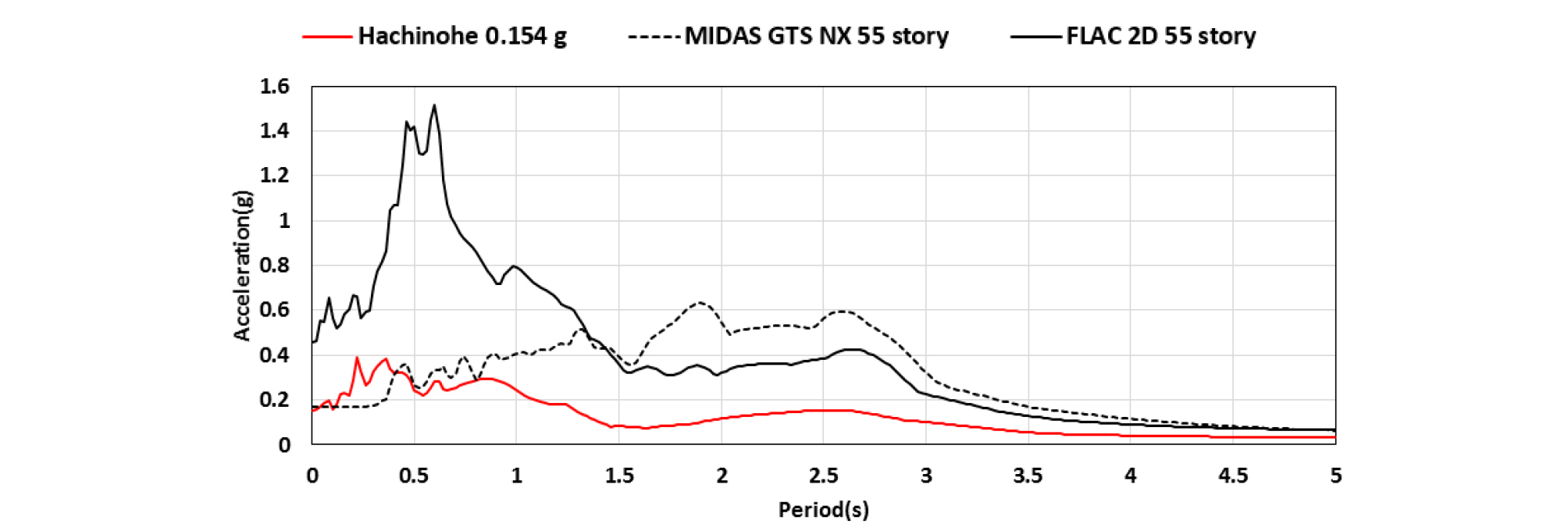
Fig. 4와 같이 해석 프로그램별 특정 지점의 가속도 이력을 FFT (Fast Fourier Transform) 변환을 통해 가속도 스펙트럼을 산출하였다. 또한 MIDAS GTS NX 동적해석과 FLAC 2D 프로그램을 사용하여 구한 초고층 건물의 최상층(55층)의 가속도 이력 결과와 입력파인 Hachinohe 지진파의 스펙트럼을 구하여 도시하였다. Fig. 4에서 보는 바와 같이 초고층 건물 55층의 가속도 스펙트럼이 MIDAS GTS NX의 경우는 2~3초에서 증폭되고, FLAC 2D의 경우 주기가 0.5초에서 증폭됨을 알 수 있다. 이는 건물과 지반의 주기가 각각 5초와 0.22초로 달리 입력되는 FLAC 2D에 비해, MIDAS GTS NX의 경우는 건물과 지반을 일체로 하여 고유치해석을 수행하여 1, 2차 고유주기로 각각 6.4초와 1.4초를 입력하였기 때문에 발생한 것으로 판단된다. 즉 MIDAS GTS NX의 경우는 1, 2차 고유주기가 2~3초인 Hachinohe 지진파의 2차 탁월주기와 근접해서 2~2.5초 사이에서 증폭된 것으로 판단된다. 반면 FLAC 2D의 경우 지반의 고유주기가 0.22초로 0.2~0.3초인 Hachinohe 지진파의 1차 탁월주기와 비슷하여 공진가능성이 높아 증폭된 것으로 판단된다.
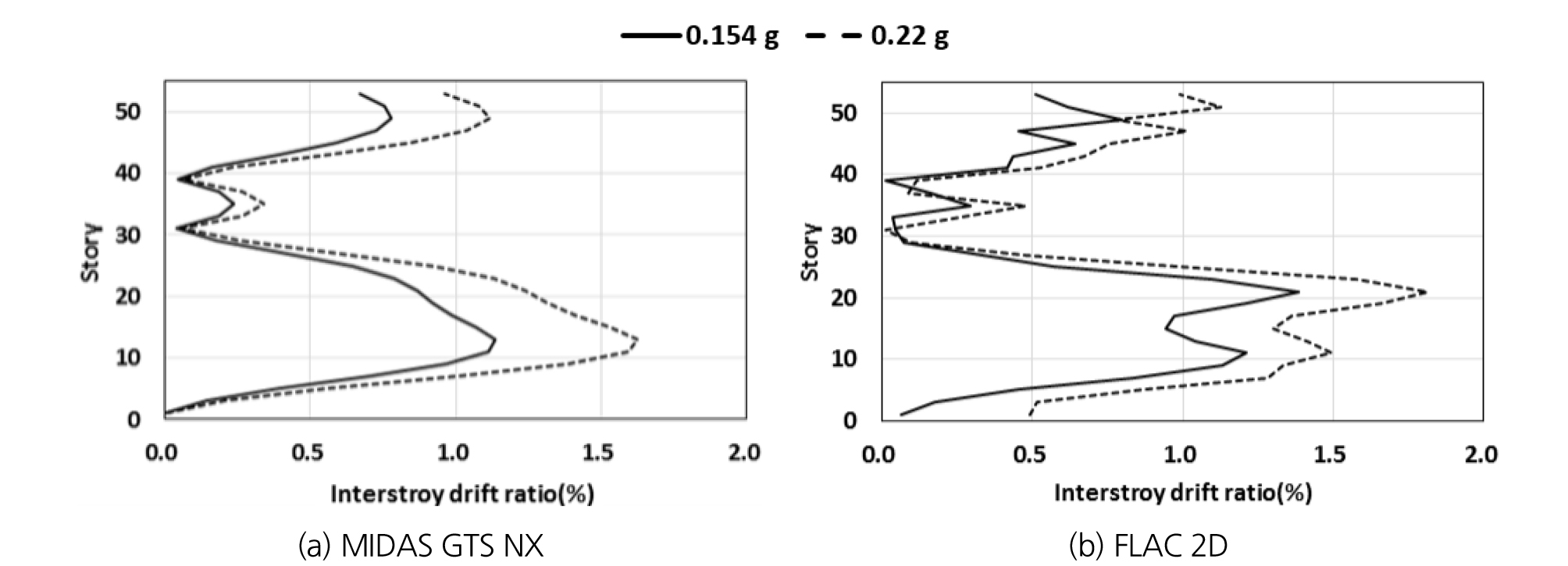
초고층 건물의 최대 수평변위 결과를 이용하여 지진 시 초고층 건물의 취약부를 판단하고자 층간변위비를 계산하고 분포도를 조사하였다. 초고층 건물 지상부 좌측 벽체에서 홀수층 단위로 최대 수평변위가 발생하는 가진 시간 12초일 때의 층간변위비를 Table 5와 같이 프로그램별로 정리하고, 그 분포를 Fig. 5에 도시하였다.
Table 5. Inter-story drift ratio of a high-rise building (excitation time = 12 seconds)
Fig. 5에서 보는 바와 같이 두 프로그램에서 구한 층간변위비 분포는 거의 유사한 것으로 나타났다. 10~20층 사이에서 층간변위비는 최대값을 나타내었고, 30~40층 사이에서 감소하였다가, 40층 이상에서는 다시 증가하는 경향을 보였다. Fig. 5(b)에서 볼 수 있듯이, MIDAS GTS NX의 해석결과 최대지반가속도가 0.22 g일 때 0.154 g보다 층간변위비가 평균 0.23% 큰 것을 확인하였다. 또한 최대지반가속도인 PGA가 0.22 g인 경우 10층과 17층 사이에서 최대 층간변위비인 1.7%가 발생하여 National Disaster Management Research Institute (2012)에서 규정한 ‘인명안전’ 수준을 초과하여 부재의 파괴가 발생할 수 있을 것으로 판단된다.
4.3 초고층 건물의 휨응력 및 취약부
지진동 시 가진 시간 12초에서 MIDAS GTS NX와 FLAC 2D에 따른 초고층 건물의 최대 휨응력을 산출하여 Table 6과 같이 도시하여 비교하였다. 두 프로그램 간 휨응력의 차이를 분석한 결과 MIDAS GTS NX 와 FLAC 2D 모두 건물 지상 지하부 인접지하구조물의 최대 휨압축응력이 허용 휨압축응력(24 MPa) 이내로 발생하여 균열 및 파괴가 발생하지 않는 것으로 나타났다. 한편, MIDAS GTS NX와 FLAC 2D의 최대 휨인장응력은 건물 지상 및 지하부 모두 허용 휨인장응력(-4 MPa)을 초과하고, 특히 건물 지상 및 지하부의 MIDAS GTS NX의 휨응력의 경우 FLAC 2D보다 압축 및 인장 모두 각각 48.5%, 45%, 크게 발생하여 균열 및 파괴의 가능성이 있는 취약한 부재가 있다고 판단하였다.
Table 6. The maximum bending stresses of above, below ground part and the adjacent underground structure (excitation time = 12 seconds)
참고로, 부재에 발생한 전단응력에 대해 허용 전단응력(2.4 MPa)과 비교하였으나, MIDAS GTS NX와 FLAC 2D 모두 모든 부재가 허용 전단응력보다 낮게 산출되어 안정한 것으로 나타났다. 따라서 상세한 추가 분석은 수행하지 않았다.
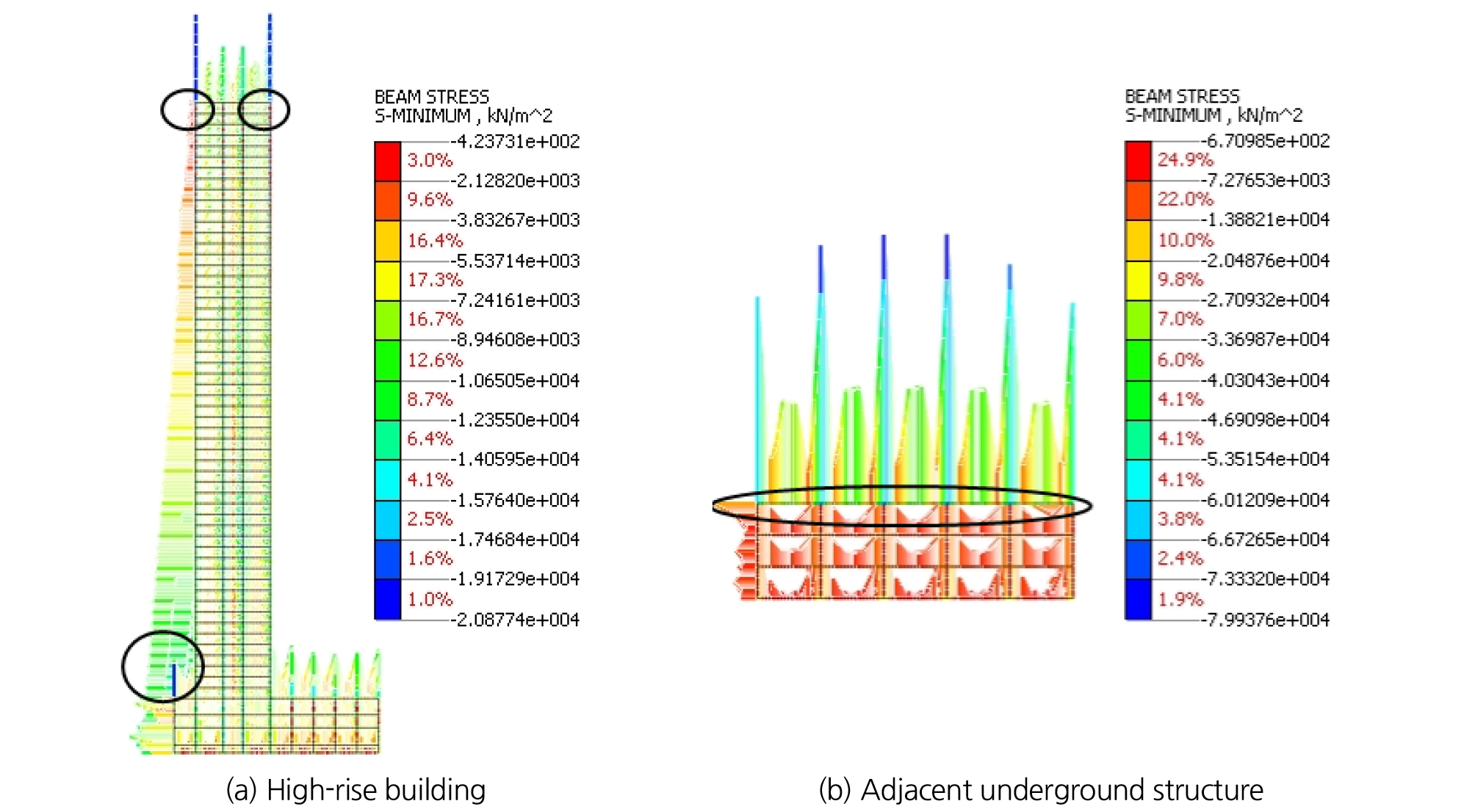
Fig. 6은 최대지반가속도가 0.154 g이고 가진 시간 12초일 때 MIDAS GTS NX 프로그램으로 수행한 초고층 건물의 지상 및 지하부와 인접지하구조물의 휨인장응력 분포도를 나타낸 것이다. 취약부의 경우 검은색 타원으로 표시하여 건물별 취약부를 파악하였다. Fig. 6(a)와 같이 초고층 건물의 경우 건물 좌 ‧ 우측 상단과 지하부 1층 좌측 벽체에서 허용 휨인장응력을 초과한 부재가 발생하였고 인접지하구조물의 경우 인접지하천정부에서 취약부가 발생하였다. 이는 지상 건물 자체의 중량 및 수평방향의 지진동으로 인하여 지하부 기둥에 인장력이 과도하게 작용하여 최대 휨인장응력이 발생한 것으로 판단된다.
또한 인접지하구조물의 경우 지진 시 지반의 거동으로 인하여 부재가 지진하중을 받는 것뿐만이 아니라 지반의 하중도 작용하여 그로 인한 최대 휨인장응력이 과도하게 산출된 것으로 판단된다. 지진 시 초고층 건물의 경우 모드형상은 1차 모드, 2차 모드로 거동하게 되어 일반적인 캔틸레버 보와 같이 지반과 접해있는 지상부 1층과 건물 최상단에서 휨인장응력이 허용값을 초과하여 발생한 것으로 판단된다. 또한 인접지하구조물의 최대 휨인장응력은 천정부에서 -79.93 MPa로 크게 발생하여 취약부로 나타났다. 이는 지진 시 지반이 안정화되지 못하고 동적하중으로 인하여 동적거동을 하게 되어 인접지하구조물 천정부에 영향을 미친 것으로 판단된다.
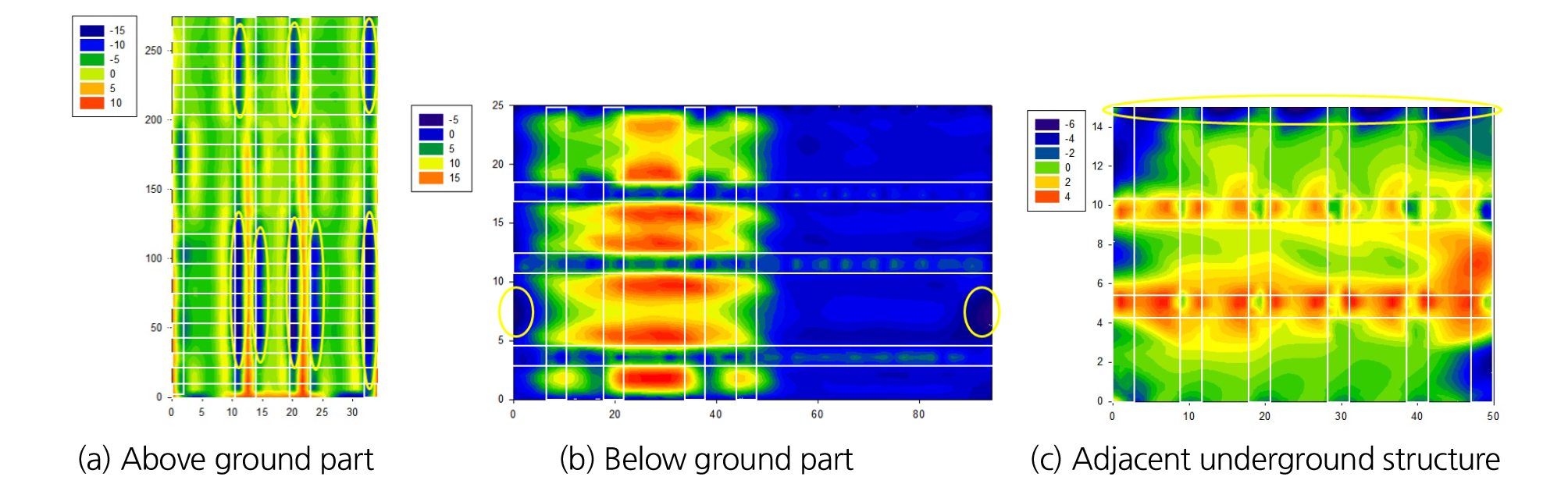
Fig. 7은 FLAC 2D에 의한 결과로 최대지반가속도가 0.154 g이고 가진 시간이 12초일 때 초고층 건물의 지상 및 지하부와 인접지하구조물의 휨인장응력 분포도를 나타낸 것이다. Fig. 7(a)와 같이 초고층 건물 상단 중앙부의 기둥 2개와 좌측 벽체에서는 인장응력이 허용 휨인장응력인 -4.0 MPa를 훨씬 초과하여 타원으로 표시된 취약한 부분이 발생하였고, 건물 내부 슬래브에서도 허용응력을 초과하는 부분이 존재함을 알 수 있었다. 한편, 초고층 건물의 지하부는 Fig. 7(b)에서 볼 수 있듯이 좌 ‧ 우측에는 인장응력이 주로 발생하였는데, 이는 지진에 의해 건물에 진동이 발생했을 때 특정 부위에서 압축응력이 발생하면 그 반대방향의 부재는 인장응력을 받기 때문이라고 판단된다. 또한 인접지하구조물의 취약부의 경우 천정부에서 최대 휨인장응력이 약 -6.63 MPa가 발생하는 것을 확인할 수 있으며, 그 이외의 부분은 압축응력을 받는 것을 확인하였다.
결과적으로 지진동 시 발생한 휨응력은 압축 및 인장 모두 MIDAS GTS NX가 FLAC 2D보다 더 크게 발생하였는데, 이는 MIDAS GTS NX에서는 소성모멘트를 고려하지 않았기 때문인 것으로 판단된다. 한편 허용응력을 초과하는 취약부는 건물 상단부 벽체 및 기둥, 지하부 벽체와 인접지하구조물 천정부 등에서 발생하는 것으로 나타나, MIDAS GTS NX와 FLAC 2D에 의한 결과가 일치함을 알 수 있었다. 반면, 지반이 연약해질수록 구조물의 휨응력 및 취약부는 더 증가할 것으로 사료된다.
5. 결 론
본 연구에서는 동적해석 시 사용되는 유한요소법에 근거한 MIDAS GTS NX 프로그램과 유한차분법에 기초한 FLAC 2D에 의한 초고층 건물 및 인접지하구조물 동적거동을 비교 ‧ 분석하였다.
1. MIDAS GTS NX가 FLAC 2D보다 최대 수평변위 값을 다소 작게 산출하였지만, 유사한 초고층 건물의 수평변위분포 양상과 층간변위비 분포를 주는 것을 알 수 있었다.
2. 한편 휨응력은 압축 및 인장 모두 MIDAS GTS NX가 FLAC 2D보다 더 크게 발생하였으나, 허용응력을 초과하는 취약부는 건물 상단부 벽체 및 기둥, 지하부 벽체와 인접지하구조물 천정부의 동일한 위치에서 발생하는 것으로 나타났다.
3. 종합적으로 판단할 때, 향후 SSI 해석을 고려한 동적해석 시 유한요소법 및 유한차분법에 근거한 프로그램을 취사선택하여 사용하는 데에 큰 문제가 없을 것으로 판단된다.
다만, 본 논문에서는 동일한 조건을 대상으로 해석을 수행한 결과를 비교 ‧ 분석하였기 때문에, 향후 지진파 종류, 대상 건물 및 지반 조건이 변할 때 초고층 건물 및 인접지하구조물의 동적해석을 수행한다면 보다 상세한 분석이 가능할 것으로 판단된다.